题目内容
【题目】如图，在三棱柱ABC－A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点.
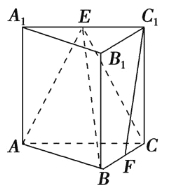
(1)求证：AB⊥平面B1BCC1； 平面ABE⊥平面B1BCC1；
(2)求证：C1F∥平面ABE；
(3)求三棱锥E－ABC的体积.
【答案】(1)详见解析(2)详见解析(3) 
【解析】
试题分析：（1）由
，
可证明AB⊥B1BCC1，进而由面面垂直的判定定理可得平面ABE⊥平面B1BCC1；（2）证明C1F∥平面ABE，只需证明四边形FGEC1为平行四边形，可得C1F∥EG；（3）利用VE-ABC=
S△ABCAA1，可求三棱锥E-ABC的体积
试题解析：（1）因为在三棱柱
中，
底面
，所以，又因为，所以
平面
，所以平面
平面
。 ......4分
（2）取
的中点
，连接
因为
分别是
、
、
的中点，所以
，且
，
。因为
且
，所以
且
，所以四边形
为平行四边形，所以
。又因为
在平面
上，且
不在平面
上，所以
平面
。 ......8分
（3）因为
，
，
，所以
，所以三棱锥
的体积
。 ......12分
练习册系列答案
53随堂测系列答案
相关题目
【题目】从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次，命中的环数如下：
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差；
(2)比较两个人的成绩，然后决定选择哪名学生参加射箭比赛.
