题目内容
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
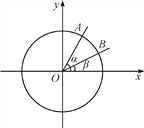
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据椭圆的基本量的关系得:![]() ,化简
,化简![]() ,
,![]() ,所以
,所以![]() ,所求直线方程
,所求直线方程![]() ;(2)设直线
;(2)设直线![]() 的方程为
的方程为![]() ,由直线与圆锥曲线的位置关系联立
,由直线与圆锥曲线的位置关系联立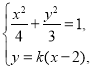 ,整理得
,整理得![]() ,
,![]() ,从而
,从而![]() ,由
,由![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立方程组得解得
,联立方程组得解得![]() ,根据大角对大边,
,根据大角对大边,![]() ,从而
,从而![]() ,化简得
,化简得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
试题解析:(1)设![]() ,由
,由![]() ,即
,即![]() ,
,
可得![]() ,
,
又![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以椭圆的方程为![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() (
(![]() ),则直线
),则直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,
由方程组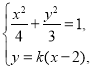 整理得
整理得![]() ,
,
解得![]() ,或
,或![]() ,
,
由题意得![]() ,从而
,从而![]() .
.
由(1)知,![]() ,设
,设![]() ,有
,有![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
因此直线![]() 的方程为
的方程为![]() .
.
设![]() ,由方程组
,由方程组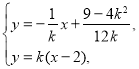
解得![]() ,
,
在△![]() 中,
中,![]() 等价于
等价于![]() ,
,
即![]() ,
,
化简得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() .
.
所以,直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 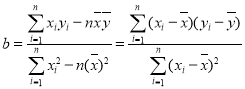 ,
, ![]() .
.