题目内容
【题目】已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=x2+2x.
(Ⅰ)求f(0)的值;
(Ⅱ)求此函数在R上的解析式;
(Ⅲ)若对任意的t∈R,不等式f(t+1)+f(m﹣2t2)<0恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)因为f(x)是定义在R上的奇函数,所以f(﹣0)=﹣f(0),f(0)=0
(Ⅱ)设x<0,则﹣x>0,∴f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x,
又∵f(x)是定义在R上的奇函数,∴f(x)=﹣f(﹣x)=﹣x2+2x,
∴ 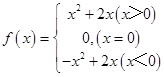 .
.
(Ⅲ)任取x1 , x2∈(0,+∞),且x1<x2 ,
则 ![]() ,
,
∵x1 , x2∈(0,+∞),且x1<x2 , ∴x1+x2+2>0,x1﹣x2<0,
∴f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在(0,+∞)上单调递增.
同理可证:函数f(x)在(﹣∞,0)上单调递增,又f(0)=0,
∴函数f(x)在R上单调递增.
∵对任意的t∈R,不等式f(t+1)+f(m﹣2t2)<0恒成立,
即f(t+1)<﹣f(m﹣2t2)=f(2t2﹣m)恒成立,
∴t+1<2t2﹣m,即 ![]() 恒成立,
恒成立,
∴ ![]() ,
,
所以,实数m的取值范围为 ![]()
【解析】(Ⅰ)f(x)是定义在R上的奇函数f(﹣0)=﹣f(0),从而可得f(0)的值;(Ⅱ)设x<0,则﹣x>0,利用x>0时,f(x)=x2+2x及f(x)=﹣f(﹣x),可求得此时f(x)的表达式,从而可得此函数在R上的解析;(Ⅲ)任取x1 , x2∈(0,+∞),且x1<x2 , 利用定义法可判断函数f(x)在R上单调递增,再将不等式f(t+1)+f(m﹣2t2)<0恒成立转化为f(t+1)<﹣f(m﹣2t2)=f(2t2﹣m)恒成立,分离参数m,利用恒成立思想可求实数m的取值范围.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案