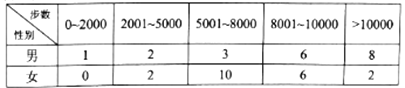
题目内容
【题目】已知函数y=x+ 
有如下性质：如果常数t＞0，那么该函数（0， 
]上是减函数，在[ ，+∞）上是增函数．
（1）已知f（x）= 
，g（x）=﹣x﹣2a，x∈[0，1]，利用上述性质，求函数f（x）的单调区间和值域．
（2）对于（1）中的函数f（x）和函数g（x），若对于任意的x1∈[0，1]，总存在x2∈[0，1]，使得g（x2）=f（x1）成立，求实数a的值．
【答案】
（1）解：f（x）= 
=2x+1+ 
﹣8，
设u=2x+1，x∈[0，1]，则1≤u≤3，则y=u+ 
﹣8，u∈[1，3]，由已知性质得，
当1≤u≤2，即0≤x≤ 
时，f（x）单调递减，所以递减区间为[0， ]
当2≤u≤3，即 ≤x≤1时，f（x）单调递增，所以递增区间为[ ，1]
由f（0）=﹣3，f（ ）=﹣4，f（1）=﹣ 
，得f（x）的值域为[﹣4，﹣3]
（2）解：由于g（x）=﹣x﹣2a为减函数，故g（x）∈[﹣1﹣2a，﹣2a]，x∈[0，1]，
由题意，f（x）的值域为g（x）的值域的子集，从而有
所以 a= 
【解析】（1）将2x+1看成整体，研究对勾函数的单调性从而求出函数的值域，以及利用复合函数的单调性的性质得到该函数的单调性；（2）对于任意的x1∈[0，1]，总存在x2∈[0，1]，使得g（x2）=f（x1）可转化成f（x）的值域为g（x）的值域的子集，建立关系式，解之即可．
【考点精析】本题主要考查了函数单调性的性质的相关知识点，需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题．
练习册系列答案
期末集结号系列答案
相关题目
