题目内容
2.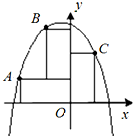 如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
分析 根据矩形的性质,利用矩形边长得出A,B,C三点的坐标,再利用待定系数法求出二次函数解析式即可.
解答 解:∵沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,
∴A点的坐标为:(-4,2),B点的坐标为:(-2,6),C点的坐标为:(2,4),
将A,B,C代入y=ax2+bx+c,
$\left\{\begin{array}{l}16a-4b+c=2\\ 4a-2b+c=6\\ 4a+2b+c=4\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=-\frac{5}{12}\\ b=-\frac{1}{2}\\ c=\frac{20}{3}\end{array}\right.$,
∴二次函数解析式为:y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
故答案为:y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
点评 此题主要考查了矩形的性质以及待定系数法求二次函数解析式,根据矩形边长得出A,B,C三点坐标是解决问题的关键.

练习册系列答案
相关题目
13.设直线l,m,平面α,β,下列条件能得出α∥β的是( )
| A. | l?α,m?α且l∥β,m∥β | B. | l?α,m?β且l∥m | ||
| C. | l⊥α,m⊥β且l∥m | D. | l∥α,m∥β且l∥m |
10.下列图象表示的函数中,不能用二分法求零点的是( )
| A. | 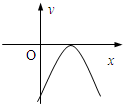 | B. | 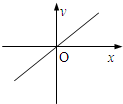 | C. | 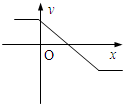 | D. | 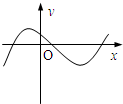 |