题目内容
12.在直角三角形ABC中,∠C=90°,AB=2,AC=1,若$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}$,则$\overrightarrow{CD}$•$\overrightarrow{CB}$=$\frac{3}{2}$.分析 如图所示,建立直角坐标系,利用数量积的坐标运算性质即可得出.
解答 解:如图所示,
A(1,0),B(0,$\sqrt{3}$),C(0,0),
∵$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}$,
∴D$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
∴$\overrightarrow{CD}$=$(\frac{1}{2},\frac{\sqrt{3}}{2})$,$\overrightarrow{CB}$=(0,$\sqrt{3}$),
∴$\overrightarrow{CD}$•$\overrightarrow{CB}$=0+$\frac{\sqrt{3}}{2}×\sqrt{3}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了数量积的坐标运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.正弦函数y=sin(x+$\frac{3π}{2}$),x∈R的图象关于( )对称.
| A. | y轴 | B. | 直线x=$\frac{3π}{2}$ | C. | 直线x=$\frac{π}{2}$ | D. | 直线x=-$\frac{π}{2}$ |
4.正整数a、b、c是等腰三角形的三边长,并且a+bc+b+ca=24,则这样的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
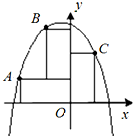 如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.