题目内容
14.对于定义在R上的函数f(x),若f(0)=1,且对任意的x∈R,都有f(x+1)-f(x)=2,则$\frac{2}{f(0)f(1)}$+$\frac{2}{f(1)f(2)}$+…+$\frac{2}{f(2014)f(2015)}$=$\frac{4030}{4031}$.分析 根据条件对任意的x∈R,都有f(x+1)-f(x)=2,得到f(x)是等差数列,求出f(x)的表达式,利用裂项法进行求解即可.
解答 解:∵任意的x∈R,都有f(x+1)-f(x)=2,
∴f(x)可以看成是以f(0)=1为首项,2为公差的等差数列,
则f(x)=1+2x,
则$\frac{2}{f(x)f(x+1)}$=$\frac{2}{(1+2x)(2x+3)}$=$\frac{1}{2x+1}$-$\frac{1}{2x+3}$,
即$\frac{2}{f(0)f(1)}$+$\frac{2}{f(1)f(2)}$+…+$\frac{2}{f(2014)f(2015)}$=1$-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+$$\frac{1}{2×2014+1}$-$\frac{1}{2×2014+3}$=1-$\frac{1}{2×2014+3}$=1-$\frac{1}{4031}$=$\frac{4030}{4031}$,
故答案为:$\frac{4030}{4031}$.
点评 本题主要考查函数值的计算,根据条件结合等差数列的通项公式,利用裂项法进行求解是解决本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.一边长为a的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒,为使方盒的容积最大,则x的值是( )
| A. | $\frac{a}{3}$ | B. | $\frac{a}{4}$ | C. | $\frac{a}{5}$ | D. | $\frac{a}{6}$ |
9.已知集合A={x|x2-5x+6<0},B={x||x|≤2},则∁RA∩B=( )
| A. | A | B. | CRA | C. | B | D. | CRB |
6.在某项测量中,测量结果X服从正态分布N(4,σ2)(σ>0),若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为( )
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.6 |
4.正整数a、b、c是等腰三角形的三边长,并且a+bc+b+ca=24,则这样的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
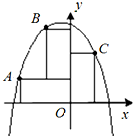 如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.
如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是y=-$\frac{5}{12}$x2-$\frac{1}{2}$x+$\frac{20}{3}$.