Question

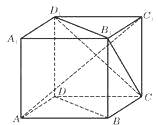
【题目】如如图，SD垂直于正方形ABCD所在的平面， ．
（1）求证：BC⊥SC；
（2）设棱SA的中点为M，求异面直线DM与SC所成角的大小．

Answer 1

【答案】
（1）证明：

所以，BC⊥SC

（2）取SB，CD，BC的中点分别为P，Q，R，连接MP，PQ，QR，PR

则 ，又

所以∠RPQ为异面直线DM，SC所成角或其补角

计算易得∠RPQ=60°，即异面直线DM，SC所成角为60°

【解析】（1）由已知中SD垂直于正方形ABCD所在的平面，我们可得BC⊥CD，进而由面面垂直的性质得到BC⊥平面SDC，再由线面垂直的性质可得BC⊥SC；（2）取SB，CD，BC的中点分别为P，Q，R，连接MP，PQ，QR，PR，由三角形中位线定理可得DM∥PQ，PR∥SC，我们可得∠RPQ为异面直线DM，SC所成角或其补角，解三角形RPQ即可得到答案．
【考点精析】通过灵活运用直线与平面垂直的性质，掌握垂直于同一个平面的两条直线平行即可以解答此题．