题目内容
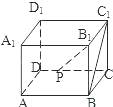
【题目】如图,ABCD﹣A1B1C1D1为正方体,下面结论错误的序号是 .
①BD∥平面CB1D1;
②AC1⊥BD;
③AC1⊥平面CB1D1;
④异面直线AD与CB1所成角为60°.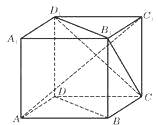
【答案】④
【解析】由正方体的性质得,BD∥B1D1 , 所以,BD∥平面CB1D1;故①正确.
由正方体的性质得 AC⊥BD,而AC是AC1在底面ABCD内的射影,由三垂线定理知,AC1⊥BD,故②正确.
由正方体的性质得 BD∥B1D1 , 由②知,AC1⊥BD,所以,AC1⊥B1D1 , 同理可证AC1⊥CB1 ,
故AC1垂直于平面CB1D1内的2条相交直线,所以,AC1⊥平面CB1D1 , 故③成立.
异面直线AD与CB1所成角就是BC与CB1所成角,故∠BCB1为异面直线AD与CB1所成角,
等腰直角三角形BCB1中,∠BCB1=45°,故④不正确.
所以答案是:④.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
相关题目