若A${\;} {n}^{2}$=4C${\;} {n-1}^{2}$.则n的值为( )A．7B．6C．5D．4 题目和参考答案——青夏教育精英家教网——

题目内容

14．若A${\;}_{n}^{2}$=4C${\;}_{n-1}^{2}$，则n的值为（　　）

A．

7

B．

6

C．

5

D．

4

分析根据排列数与组合数的公式，列出方程，求出n的值即可．

解答解：∵A${\;}_{n}^{2}$=4C${\;}_{n-1}^{2}$，
∴n（n-1）=4×$\frac{（n-1）（n-2）}{2×1}$，
n=4；
∴n的值为4．
故选：D．

点评本题考查了排列与组合公式的应用问题，是基础题目．

练习册系列答案

励耘新中考系列答案

新课标新中考浙江中考系列答案

优加学案赢在中考系列答案

优能英语完形填空与阅读理解系列答案

初中英语阅读教程系列答案

领军中考系列答案

名师面对面中考满分策略系列答案

决战中考系列答案

新题型题库系列答案

中考复习与指导系列答案

相关题目

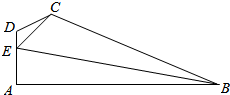如图所示，在平面四边形ABCD中，$\overrightarrow{DA}•\overrightarrow{AB}=0，|{\overrightarrow{EC}}|=\sqrt{7}，|{\overrightarrow{AD}}|=3，\overrightarrow{AE}=2\overrightarrow{ED}$，$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$，$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$．
（1）求△CDE的面积S；
（2）求$|{\overrightarrow{BE}}|$．

5．设函数f（x）=$\frac{1}{3}$x³-$\frac{a}{2}$x²+bx+c，曲线y=f（x）在点（0，f（0））处的切线方程为y=1．
①求b，c的值；
②已知a∈R，求函数f（x）的单调区间．

2．函数f（x）=x+$\frac{1}{x-1}$（x＞1）的最小值是3；此时x=2．

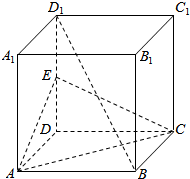在长方体ABCD-A₁B₁C₁D₁中，E为DD₁的中点．
（1）判断BD₁与平面AEC的位置关系，并证明你的结论．
（2）若AB=BC=$\sqrt{3}$，CC₁=2，求异面直线AE、BD₁所成的角的余弦值．

19．给出下列四个不等式：①当x∈R时，sin x+cos x＞-$\frac{3}{2}$；②对于正实数x，y及任意实数α，有xsin2α•ycos2α＜x+y；③x是非0实数，则|x+$\frac{1}{x}$|≥2；④当α，β∈（ 0，$\frac{π}{2}$）时，|sin α-sin β|≤|α-β|．在以上不等式中不成立的有（　　）

6．设k＞0，若关于x的不等式kx+$\frac{4}{x-1}$≥12在（1，+∞）上恒成立，则k的最小值为4．

3．若方程a^x-x-a=0有两个实数解，则a的取值范围是（　　）

16．设{a_n}是首项为1的正项数列，且$（{n+1}）a_{n+1}^2-na_n^2+{a_{n+1}}{a_n}=0$（n=1，2，3，…），则它的通项公式是a₁₀₀=（　　）

$\frac{1}{100}$

$\frac{1}{101}$