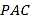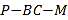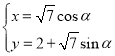题目内容
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
【答案】(1)分布列见解析,2.6(2)40000尾
【解析】
(1)由题意得随机变量![]() 的所有可能取值为0,1,2,3,利用相互独立事件同时发生的概率,可计算
的所有可能取值为0,1,2,3,利用相互独立事件同时发生的概率,可计算![]() 的值,进而得到分布列和期望;
的值,进而得到分布列和期望;
(2)依题意知一尾乙种鱼苗最终成活的概率为![]() ,计算一尾乙种鱼苗的平均收益,进而计算
,计算一尾乙种鱼苗的平均收益,进而计算![]() 尾乙种鱼苗最终可获得的利润,再解不等式,即可得答案.
尾乙种鱼苗最终可获得的利润,再解不等式,即可得答案.
(1)记随机变量![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
| 0.002 | 0.044 | 0.306 | 0.648 |
![]() .
.
(2)根据已知乙种鱼苗自然成活的概率为0.9,
依题意知一尾乙种鱼苗最终成活的概率为![]() ,
,
所以一尾乙种鱼苗的平均收益为![]() 元.
元.
设购买![]() 尾乙种鱼苗,
尾乙种鱼苗,![]() 为购买
为购买![]() 尾乙种鱼苗最终可获得的利润,
尾乙种鱼苗最终可获得的利润,
则![]() ,解得
,解得![]() .
.
所以需至少购买40000尾乙种鱼苗,才能确保获利不低于37.6万元.

【题目】某连锁餐厅新店开业,打算举办一次食品交易会,招待新老顾客试吃.项目经理通过查阅最近![]() 次食品交易会参会人数
次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) |
|
|
|
|
|
原材料(袋) |
|
|
|
|
|
(1)根据所给![]() 组数据,求出
组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为
,投入使用的每袋原材料相应的销售收入为![]() 元,多余的原材料只能无偿返还,据悉本次交易大会大约有
元,多余的原材料只能无偿返还,据悉本次交易大会大约有![]() 万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.