题目内容
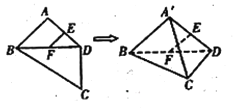
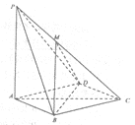
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
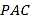
图一
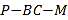
图二
【答案】(1)见解析(2)![]()
【解析】
(1)设AC的中点为O,证明PO垂直AC,OB,结合平面与平面垂直判定,即可.(2)建立直角坐标系,分别计算两相交平面的法向量,结合向量的数量积公式,计算夹角,即可.
(Ⅰ)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
由题意,得![]() ,
,
![]() ,
,![]() .
.
因为在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
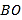
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
且![]() ,
,
所以当![]() 最短时,即
最短时,即![]() 是
是![]() 的中点时,
的中点时,![]() 最大.
最大.
由![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是以
,于是以
![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图示空间直角坐标系,
轴建立如图示空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由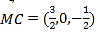 得:
得:![]() .
.
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由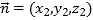 得:
得:![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
![]() .
.
由图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
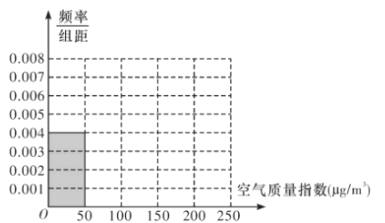
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。