Question

【题目】已知数列{an}的前n项和为Sn，a1＝1，an＞0，Sn2＝an+12﹣λSn+1，其中λ为常数.

（1）证明：Sn+1＝2Sn+λ；

（2）是否存在实数λ，使得数列{an}为等比数列，若存在，求出λ；若不存在，说明理由.

Answer 1

【答案】（1）证明见解析；（2）存在，λ＝1

【解析】

（1）利用已知条件通过an+1＝Sn+1﹣Sn，推出Sn+1（Sn+1﹣2Sn﹣λ）＝0，然后证明：Sn+1＝2Sn+λ；.

（2）求出数列的通项公式，利用数列是等比数列，求解即可.

（1）证明：∵an+1＝Sn+1﹣Sn，，

∴，

∴Sn+1（Sn+1﹣2Sn﹣λ）＝0，

∴an＞0，∴Sn+1＞0，

∴Sn+1﹣2Sn﹣λ＝0；

∴Sn+1 ＝ 2Sn+λ

（2）解：∵Sn+1＝2Sn+λ，Sn＝2Sn﹣1+λ（n≥2），

相减得：an+1＝2an（n≥2），∴{an}从第二项起成等比数列，

∵S2＝2S1+λ即a2+a1＝2a1+λ，

∴a2＝1+λ＞0得λ＞﹣1，

∴an，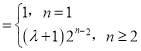

若使{an}是等比数列

则，∴2（λ+1）＝（λ+1）2，

∴λ＝1经检验得符合题意.