题目内容
已知函数f(x)=x2+ax+b,当p,q满足p+q=1时,证明:pf(x)+qf(y)≥f(px+qy)对于任意实数x,y都成立的充要条件是0≤p≤1.
见解析
证明:pf(x)+qf(y)-f(px+qy)
=p(x2+ax+b)+q(y2+ay+b)-(px+qy)2-a(px+qy)-b
=p(1-p)x2+q(1-q)y2-2pqxy
=pq(x-y)2(因为p+q=1).
充分性:若0≤p≤1,q=1-p∈[0,1].
所以pq≥0,所以pq(x-y)2≥0,
所以pf(x)+qf(y)≥f(px+qy).
必要性:若pf(x)+qf(y)≥f(px+qy),
则pq(x-y)2≥0,
因为(x-y)2≥0,所以pq≥0.
即p(1-p)≥0,所以0≤p≤1.
综上,原命题成立.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
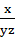 +
+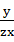 +
+ ≥
≥ +
+ +
+ .
. +
+ +
+ ≥9.
≥9.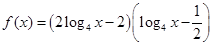 。
。 时,求该函数的值域;
时,求该函数的值域; 对于
对于 恒成立,求
恒成立,求 的取值范围.
的取值范围.


 ,b=1+x,c=
,b=1+x,c= ,则其中最大的是 .
,则其中最大的是 .
 (x>0)的最小值是 ( )
(x>0)的最小值是 ( )


