题目内容
【题目】已知⊙O:x2+y2=2,⊙M:(x+2)2+(y+2)2=2,点P的坐标为(1,1).
(1)过点O作⊙M的切线,求该切线的方程;
(2)若点Q是⊙O上一点,过Q作⊙M的切线,切点分别为E,F,且∠EQF= ![]() ,求Q点的坐标;
,求Q点的坐标;
(3)过点P作两条相异直线分别与⊙O相交于A,B,且直线PA与直线PB的倾斜角互补,试判断直线OP与AB是否平行?请说明理由.
【答案】
(1)解:设切线方程为:y=kx,则 ![]()
切线方程为 ![]() 或
或 ![]()
(2)解:由题知,∠EQF= ![]() ,即QM=2ME,设Q(x,y),则Q的轨迹为:
,即QM=2ME,设Q(x,y),则Q的轨迹为: 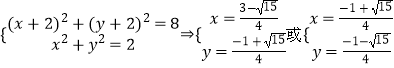
即 ![]()
(3)解:由题设lPA:y﹣1=k(x﹣1)则lPB:y﹣1=﹣k(x﹣1)
由 ![]() ;
;
同理 ![]()
又kOP=1kAB=kOP直线OP与AB平行
【解析】(1)设切线方程为:y=kx,则 ![]() ,即可求该切线的方程;(2)题知,∠EQF=
,即可求该切线的方程;(2)题知,∠EQF= ![]() ,即QM=2ME,求出Q的轨迹方程,即可求Q点的坐标;(3)求出A,B的坐标,利用斜率公式证明kAB=kOP直线OP与AB平行.
,即QM=2ME,求出Q的轨迹方程,即可求Q点的坐标;(3)求出A,B的坐标,利用斜率公式证明kAB=kOP直线OP与AB平行.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目