Question

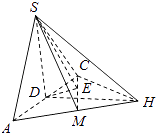
【题目】如图在三棱锥S﹣ABC中，△ABC是边长为2的正三角形，平面SAC⊥平面ABC，SA=SC= ，M为AB的中点．
（I）证明：AC⊥SB；
（Ⅱ）求点B到平面SCM的距离．

Answer 1

【答案】（Ⅰ）证明：如图，取AC的中点D，连接DS，DB．∵SA=SC，BA=BC，
∴AC⊥DS，且AC⊥DB，DS∩DB=D，
∴AC⊥平面SDB，又SB平面SDB，
∴AC⊥SB．
（Ⅱ）解：∵SD⊥AC，平面SAS⊥平面ABC，
∴SD⊥平面ABC．
如图，过D作DE⊥CM于E，连接SE，则SE⊥CM，
∴在Rt△SDE中，SD=1，DE= ，
∴SE= ．CM是边长为2的正△ABC的中线，∴CM= ．
∴ = ．
= ．
设点B到平面SCM的距离为h，
则由VB﹣SCM=VS﹣BCM得 ，
∴ ．

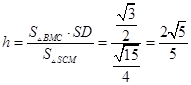【解析】（Ⅰ）欲证AC⊥SB，取AC中点D，连接DS、DB，根据线面垂直的性质定理可知，只须证AC⊥SD且AC⊥DB，即得；（Ⅱ）设点B到平面SCM的距离为h，利用等体积法：VB﹣SCM=VS﹣CMB ， 即可求得点B到平面SCM的距离．
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识，掌握垂直于同一个平面的两条直线平行．