题目内容
【题目】已知梯形ABCD,AB∥CD,且AB=AD=2,CD=3.
(1)用向量 ![]() 、
、 ![]() 表示向量
表示向量 ![]() ;
;
(2)若AD⊥AB,求向量 ![]() 、
、 ![]() 夹角的余弦值.
夹角的余弦值.
【答案】
(1)解:∵梯形ABCD,AB∥CD,且AB=AD=2,CD=3,∴ ![]() ,
,
∴ ![]() =﹣
=﹣ ![]() +
+ ![]() ,∴
,∴ ![]() =3
=3 ![]() ﹣2
﹣2 ![]()
(2)解:以D点为原点,以DC所在直线为x轴,以DA所在直线为y轴,建立直角坐标系,
则D(0,0),A(0,2),C(3,0),B(2,2),
∴ ![]() =(3,﹣2),
=(3,﹣2), ![]() =(﹣2,﹣2),
=(﹣2,﹣2), ![]() =﹣6+4=﹣2,
=﹣6+4=﹣2,
∴cos< ![]() >=
>= 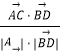 =
= ![]() =﹣
=﹣ ![]()
【解析】(1)利用两个向量的加减法的几何意义,可得用向量 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 的解析式.(2)建立坐标系,根据两个向量坐标形式的运算,以及两个向量的数量积的定义,求得cos<
的解析式.(2)建立坐标系,根据两个向量坐标形式的运算,以及两个向量的数量积的定义,求得cos< ![]() >=
>= 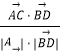 的值.
的值.
【考点精析】本题主要考查了数量积表示两个向量的夹角的相关知识点,需要掌握设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则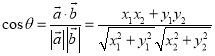 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目
