题目内容
1.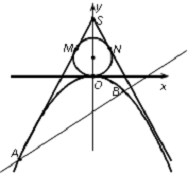 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.(1)求抛物线C和两切线的方程;
(2)设抛物线的焦点为F,过点P(0,-2)的直线与抛物线相交于A,B两点,与抛物线的准线交于点C(其中点B靠近点C),且|AF|=5,求△BCF与△ACF的面积之比.
分析 (1)1)设切线方程为y=kx+3,即 kx-y+3=0,圆心到直线的距离为d=1,求出k,可得切线方程,代入抛物线方程,利用△=0,求出抛物线的方程;
(2)设A(x1,y1),B(x2,y2).由|AF|=5,可得-y2+1=5,解得y2,代入抛物线方程可得x2.A,P,M三点共线,求出B的坐标,即可求出△BCF与△ACF的面积之比.
解答 解:(1)设切线方程为y=kx+3,即 kx-y+3=0,
圆Q:x2+y2-2y=0的圆心为(0,1),半径为1,圆心到直线的距离为d=$\frac{2}{\sqrt{{k}^{2}+1}}$=1,
∴k=$±\sqrt{3}$,
∴两切线的方程y=$±\sqrt{3}$x+3,
代入x2=-2py,可得x2±2$\sqrt{3}$px+6p=0,
△=12p2-24p=0,∴p=2,
∴抛物线C的方程x2=-4y;…(7分)
(2)设A(x1,y1),B(x2,y2).
由|AF|=5,可得-y2+1=5,
解得y2=-4,代入抛物线方程可得x2=-4.
∴A(-4,-4).
∵A,P,M三点共线,∴B(2,-1),
∴△BCF与△ACF的面积之比=$\frac{|BC|}{|AC|}$=$\frac{1+1}{4+1}$=$\frac{2}{5}$.
点评 本题考查了抛物线的定义及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.如图,三个边长为2的等边三角形有一条边在同一条直线上,边B3C3上有10个不同的点P1,P2,…P10,记mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$(i=1,2,…,10),则m1+m2+…+m10的值为( )

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
10.若cosθ=-$\frac{{\sqrt{5}}}{5}$,θ∈[0,π],则tanθ=( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
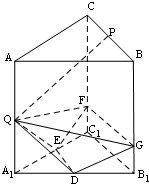 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3. 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.