题目内容
3.已知函数f(x)=14x+214x+2(x∈R).(1)若数列{an}的通项公式为an=f(nmnm)(m∈N+,n=1,2,…,m),求数列{an}的前m项和Sm
(2)设数列{bn}满足:b1=1313,bn+1=bn2+bn.设Tn=1b1+11b1+1+1b2+11b2+1+…+1bn+11bn+1.若(1)中的Sn满足对任意不小于2的正整数n,Sn<Tn恒成立,试求m的最大值.
分析 (1)通过f(x)=f(1-x)=1212,可得关系式ak+am-k=1212,从而Sm=a1+a2+…+am-1+am=am-1+am-2+…+a1+am,计算即得结论;
(2)通过题意可知11+bn11+bn=1bn1bn-1bn+11bn+1,从而Tn=3-1bn+11bn+1、数列{bn}是单调递增数列,利用T2≥T2,计算即得结论.
解答 解:(1)由题可知,f(x)=f(1-x)=1212,
所以f(kmkm)+f(1-kmkm)=1212(1≤k≤m-1),
即f(kmkm)+f(m−kmm−km)=1212,∴ak+am-k=1212,
由Sm=a1+a2+…+am-1+am ①
得Sm=am-1+am-2+…+a1+am ②
由①+②,得:2Sm=1212(m-1)+2am=m−12m−12+2×1616=m2m2-1616,
∴Sm=112112(3m-1);
(2)∵b1=1313,bn+1=bn2bn2+bn=bn(bn+1),
∴对任意的m∈N+,bn>0,有:
1bn+11bn+1=1bn(bn+1)=1bn-11+bn,即11+bn=1bn-1bn+1,
∴Tn=1b1-1b2+1b2-1b3+…+1bn-1bn+1=1b1-1bn+1=3-1bn+1,
∵bn+1-bn=bn2>0,∴数列{bn}是单调递增数列,
∴Tn关于n递增.当n≥2,且n∈N+时,Tn≥T2,
∵b1=13,b2=13(13+1)=49,b3=49(49+1)=5281,
∴T2≥T2=3-1b3=7552,
∴Sm<7552,即112(3m-1)<7552,
∴m<23839=6439,∴m的最大值为6.
点评 本题考查求数列的递推关系及求和,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 180 | B. | 60√3 | C. | 45 | D. | 15√3 |
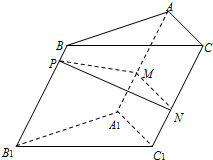 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF•EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
(3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去.
| 勾股定理的类比 | 三角形ABC | 四面体O-ABC |
| 条件 | AB⊥AC | OA、OB、OC两两垂直 |
| 结论 | AB2+AC2=BC2 | ? |
| 品牌 | 甲 | 乙 | |||
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 数量(件) | 2 | 3 | 45 | 5 | 45 |
| 每件利润(百元) | 1 | 2 | 3 | 1.8 | 2.9 |
(Ⅰ)从该厂生产的甲、乙品牌产品中随机各抽取一件,求其至少有一件首次出现故障发生在保修期内的概率;
(Ⅱ)若该厂生产的家电均能售出,记生产一件甲品牌的利润为X1,生产一件乙品牌家电的利润为X2,分别求X1,X2的分布列;
(Ⅲ)该厂预计今后这两种品牌家电销量相当,由于资金限制,只能生产其中一种品牌的家电.若从经济效益的角度考虑,你认为应生产哪种品牌的家电?说明理由.