题目内容
16.一个袋中装有1只红球、2只绿球,从中随机抽取2只球,则恰有1只红球的概率是$\frac{2}{3}$.分析 利用古典概型的概率公式求概率即可.
解答 解:装有1只红球、2只绿球的袋中随机抽取2个球,共从C32=3有种.
若有一个红球,则有C21=2种,
故恰有1只红球的概率是$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查古典概型的概率公式,要求熟练掌握

练习册系列答案
相关题目
6.已知an=($\frac{1}{2}$)n,把数列{an}的各项排列成如下的三角形状,

记A(m,n)表示第m行的第n个数,则A(10,13)=( )

记A(m,n)表示第m行的第n个数,则A(10,13)=( )
| A. | ${(\frac{1}{2})^{93}}$ | B. | ${(\frac{1}{2})^{92}}$ | C. | ${(\frac{1}{2})^{94}}$ | D. | ${(\frac{1}{2})^{112}}$ |
7.过两点(-1,0),(0,1)的直线方程为:( )
| A. | x-y+1=0 | B. | x-y-3=0 | C. | 2x-y=0 | D. | 2x-y-3=0 |
4.一只蚂蚁在三边长分别为3、4、5的三角形面上自由爬行,某时刻该蚂蚁距离三角形的三个顶点的距离不超过1的概率为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
8.某同学参加4门学科的学业水平考试,假设该同学第一门学科取得优秀成绩的概率为$\frac{2}{3}$,第二门学科取得优秀成绩的概率为$\frac{4}{5}$,第三、第四门学科取得优秀成绩的概率分别为m,n(m>n),且不同学科是否取得优秀成绩相互独立,记ξ为该同学取得优秀成绩的课程数,其分布列为如下表:
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求m,n的值;
(3)求数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{120}$ | x | y | z | $\frac{1}{5}$ |
(2)求m,n的值;
(3)求数学期望Eξ.
5.有2人从一座6层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该2人在不同层离开电梯的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
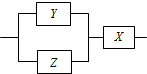 如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.
如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.