题目内容
11.已知tanα=$\frac{1}{2}$,求下列式子的值.(1)$\frac{4sinα-cosα}{sinα+cosα}$
(2)sin2α-sin2α
分析 (1)原式分子分母除以cosα,利用同角三角函数间基本关系化简,将tanα的值代入计算即可求出值;
(2)原式分母看做“1”,利用同角三角函数间基本关系化简,将tanα的值代入计算即可求出值.
解答 解:(1)∵tanα=$\frac{1}{2}$,
∴原式=$\frac{4tanα-1}{tanα+1}$=$\frac{4×\frac{1}{2}-1}{\frac{1}{2}+1}$=$\frac{2}{3}$;
(2)∵tanα=$\frac{1}{2}$,
∴原式=$\frac{si{n}^{2}α-2sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α-2tanα}{ta{n}^{2}α+1}$=$\frac{\frac{1}{4}-1}{\frac{1}{4}+1}$=-$\frac{3}{5}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
1.在△ABC中,已知a2-b2-c2=$\sqrt{2}$bc,则角B+C等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
19.计算sin(-240°)的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
6.阅读如图所示的程序框图,运行相应的程序,则输出的s的值为( )
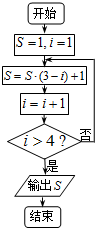

| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
20.采用系统抽样的方法从2005个个体中抽取一个容量为50的样本,则抽样间隔和随机剔除的个体数分别为
( )
( )
| A. | 40,5 | B. | 50,5 | C. | 5,40 | D. | 5,50 |
