题目内容
在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
由正弦定理得
=
=
=2cosC,即cosC=
.
由余弦定理得cosC=
=
,
∵a+c=2b,
∴cosC=
=
,
∴
=
.
整理得2a2-5ac+3c2=0,解得a=
c,a=c(舍去因为A=2C)又a+c=2b,
所以a:b=6:5.所以a:b:c=6:5:4
三角形的三边之比为:6:5:4.
| a |
| c |
| sinA |
| sinC |
| sin2C |
| sinC |
| a |
| 2c |
由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| (a+c)(a-c)+b2 |
| 2ab |
∵a+c=2b,
∴cosC=
2b(a-c)+b•
| ||
| 2ab |
2(a-c)+
| ||
| 2a |
∴
| a |
| 2c |
2(a-c)+
| ||
| 2a |
整理得2a2-5ac+3c2=0,解得a=
| 3 |
| 2 |
所以a:b=6:5.所以a:b:c=6:5:4
三角形的三边之比为:6:5:4.

练习册系列答案
相关题目
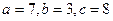 ,则其面积等于( )
,则其面积等于( )


