题目内容

1．设a=${∫}_{0}^{π}$（sinx-cosx）dx，若（1-ax）8=a0+a1x+a2x2+…+a8x8，则a0+a1+a2+…+a8=1．

分析 首先通过已知求出a，然后求展开式的系数和．

解答 解：a=${∫}_{0}^{π}$（sinx-cosx）dx=（-cosx-sinx）|${\;}_{0}^{π}$=2，
所以（1-ax）8=（1-2x）8=a0+a1x+a2x2+…+a8x8，令x=1，则a0+a1+a2+…+a8=1；
故答案为：1．

点评 本题考查了定积分的计算以及二项式定理的运用；求二项展开式的系数的有关问题时，经常用到赋值法．

练习册系列答案
相关题目
11．执行如图所示的程序框图，如果输入的t=0.01，则输出的n=（　　）
A．5B．6C．7D．8
12．已知关于x的一次函数y=ax+b，
（1）设集合P={-2，-1，1，2，3}和Q={-2，0，3}，分别从集合P和Q中随机取一个数作为a和b，求函数y=ax+b是增函数的概率；
（2）实数a，b满足条件$\left\{{\begin{array}{l}{-1≤a≤1}\\{-1≤b≤1}\\{a+b-1≤0}\end{array}}\right.$求函数y=ax+b的图象经过二、三、四象限的概率．
9．参数方程$\left\{\begin{array}{l}{x=\frac{2-3t}{1+t}}\\{y=\frac{1+4t}{1+t}}\end{array}\right.$，化成普通方程是3x+5y-11=0（x≠-3）．
16．已知椭圆的标准方程为：$\frac{x^2}{4}+\frac{y^2}{3}=1$，一个过点P（2，-3）的双曲线的长轴的端点为椭圆的焦点，求双曲线的标准方程．
6．下列类比推理的结论正确的是（　　）
①类比“实数的乘法运算满足结合律”，得到猜想“向量的数量积运算满足结合律”；
②类比“平面内，同垂直于一直线的两直线相互平行”，得到猜想“空间中，同垂直于一直线的两直线相互平行”；
③类比“设等差数列{an}的前n项和为Sn，则S4，S8-S4，S12-S8成等差数列”，得到猜想“设等比数列{bn}的前n项积为Tn，则T4，$\frac{{T}_{8}}{{T}_{4}}$，$\frac{{T}_{12}}{{T}_{8}}$成等比数列”；
④类比“设AB为圆的直径，p为圆上任意一点，直线PA，PB的斜率存在，则kPA．kPB为常数”，得到猜想“设AB为椭圆的长轴，p为椭圆上任意一点，直线PA，PB的斜率存在，则kPA．kPB为常数”．
A．①②B．③④C．①④D．②③
13．下列函数的最小值为2的是 （　　）
A．y=x+$\frac{1}{x}$B．y=sinx+$\frac{1}{sinx}$（0＜x＜$\frac{π}{2}$）
C．y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$D．y=tanx+$\frac{1}{tanx}$（0＜x＜$\frac{π}{2}$）
10．阅读如图的程序框图，则输出的S（　　）
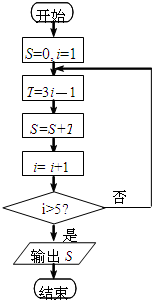
A．6B．14C．26D．40
11．空间直角坐标系中，A（1，2，3），B（-2，-1，6），C（3，2，1），D（4，3，0），则直线AB与CD的位置关系是平行．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网