题目内容
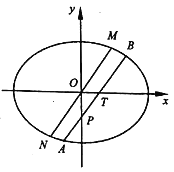
【题目】如图,在平面直角坐标系![]() 中,焦点在
中,焦点在![]() 轴上的鞘园C:
轴上的鞘园C:![]() 经过点
经过点![]() ,且
,且![]() 经过点
经过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆C与A、B两点(A在
交椭圆C与A、B两点(A在![]() 轴下方).
轴下方).
(1)求椭圆C的方程;
(2)过点![]() 且平行于
且平行于![]() 的直线交椭圆于点M、N,求
的直线交椭圆于点M、N,求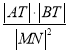 的值;
的值;
(3)记直线![]() 与
与![]() 轴的交点为P,若
轴的交点为P,若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由题意得e2![]() ,
,![]() .又a2=b2+c2,
.又a2=b2+c2,![]() ,解得b2;
,解得b2;
(2)设A(x1,y1),B(x2,y2).设直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程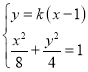 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程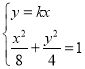 ,消去y得(2k2+1)x2=8,由MN∥l,得
,消去y得(2k2+1)x2=8,由MN∥l,得![]() 由(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]
由(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]![]() .得(xM﹣xN)2=4x2
.得(xM﹣xN)2=4x2![]() 即可;
即可;
(3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),从而 ![]() ,由
,由![]() 得
得![]()
即 ![]() ①,由(2)知
①,由(2)知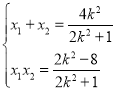 ②,由①②得
②,由①②得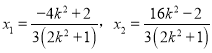 50k4﹣83k2﹣34=0,解得k2.
50k4﹣83k2﹣34=0,解得k2.
(1)因为椭圆C:![]() 1经过点
1经过点![]() 所以
所以![]() .
.
又∵a2=b2+c2,![]() ,解得b2=4或b2=8(舍去).
,解得b2=4或b2=8(舍去).
所以椭圆C的方程为![]() .
.
(2)设A(x1,y1),B(x2,y2).
因为T(1,0),则直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程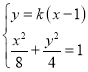 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
所以x1+x2![]() ,x1x2
,x1x2![]() .
.
因为MN∥l,所以直线MN方程为y=kx,
联立直线MN与椭圆方程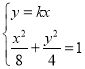
消去y得(2k2+1)x2=8,
解得x2![]()
因为MN∥l,所以![]()
因为(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]![]() .
.
(xM﹣xN)2=4x2![]() .
.
所以![]() .
.
(3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),
从而 ![]() ,
,
∵![]() ,
,![]() ①
①
由(2)知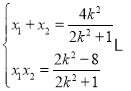 ②
②
由①②得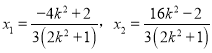
代入x1x2![]() 50k4﹣83k2﹣34=0,解得k2=2或k2
50k4﹣83k2﹣34=0,解得k2=2或k2![]() (舍).
(舍).
又因为k>0,所以k![]() .
.

【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解汽车通过某一段公路时的车辆行驶情况,现随机抽测了通过这段公路的200辆汽车的行驶速度(单位:km/h),所得数据均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
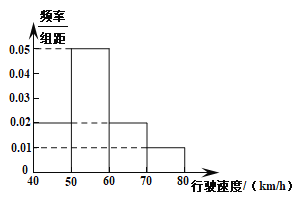
(1)求被抽测的200辆汽车的平均行驶速度.
(2)已知该路段属于事故高发路段,交警部门对此路段过往车辆限速60 km/h,并且对于超速行驶车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.
罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 500元 |
求被抽测的200辆汽车中超速10%~20%的车辆数.
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)