题目内容
【题目】如图，直三棱柱ABC-A1B1C1中，
且
，E是棱CC1中点，F是AB的中点.
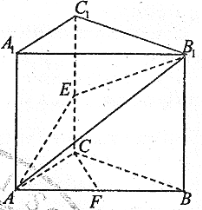
（1）求证：CF//平面AEB1；
（2）求点B到平面AEB1的距离.
【答案】(1)见解析；(2)
.
【解析】
（1）取AB1中点G，连结EG、FG，推导出四边形CEGF为平行四边形，从而CF∥EG，由此能证明CF∥平面AEB1；（2）推导出CF⊥AB，CF⊥BB1，推导出E到平面ABB1的距离等于C到平面ABB1的距离等于1，设点B到平面A的距离为d．由
，能求出点B到平面A的距离．
（1）取
中点
，连结
，则
∥
且
.
∵当
为
中点时，
∥且
，
∴∥且
.
∴四边形
为平行四边形，则
∥
又∵
，
，
∴
平面
；
（2）∵
中，
，是
中点
∴
.
又∵直三棱柱
中，
，
，
∴
，且
到
的距离为
.
∵
平面
∴到的距离等于到的距离等于
.
设点
到平面
的距离为
.
∵
∴
，易求
，
，解得
.
∴点到平面的距离为
.
【题目】“中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
.
(1)请将上面的列联表补充完整(直接写结果，不需要写求解过程)，并据此资料分析反感“中国式过马路”与性别是否有关？
(2)若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．
附：K2＝
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
【题目】抽样得到某次考试中高二年级某班8名学生的数学成绩和物理成绩如下表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
(1) 求y与x的线性回归直线方程(系数保留到小数点后两位)．
(2) 如果某学生的数学成绩为83分，预测他本次的物理成绩．
(参考公式：回归直线方程为
＝
x＋
，其中
，a＝
－b
.参考数据：＝77.5，
≈84.9，
，
.)
