题目内容
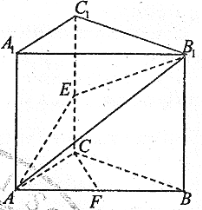
【题目】如图,在平行六面体ABCD-A1B1C1D1中,E,F,G分别是A1D1,D1D,D1C1的中点.
(1)求证:EG∥AC;
(2)求证:平面EFG∥平面AB1C.
【答案】（1）见解析；（2）见解析
【解析】
(1)选出向量的基底，利用向量共线基本定理，可判断两条直线平行。
(2)根据向量的线性运算，可判断直线与直线的平行，进而得到平面与平面的平行。
证明把{
}作为空间的一个基底.
(1)因为
,所以
=2
.
所以EG∥AC.
(2)由(1)知EG∥AC,又AC平面AB1C,EG平面AB1C,所以EG∥平面AB1C.
因为
,所以
=2
.所以FG∥AB1.
又AB1平面AB1C,FG平面AB1C,
所以FG∥平面AB1C.
又EG∩FG=G,所以平面EFG∥平面AB1C.
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
【题目】若定义在
上的函数
满足
，且
是奇函数，现给出下列4个结论：①是周期为4的周期函数；
②的图象关于点
对称；
③是偶函数；
④的图象经过点
,其中正确结论的序号是__________（请填上所有正确的序号）．
【题目】某风景区水面游览中心计划国庆节当日投入之多3艘游船供游客观光，过去10年的数据资料显示每年国庆节当日客流量X（单位：万人）都大于1，并把客流量分成三段整理得下表：
国庆节当日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
频数 | 2 | 4 | 4 |
以这10年的数据资料记录的隔断客流量的频率作为每年客流量在隔断发生的概率，且每年国庆节当日客流量相互独立．
（1）求未来连续3年国庆节当日中，恰好有1年国庆节当日客流量超过5万人的概率；
（2）该水面游览中心希望投入的游船尽可能使用，但每年国庆节当日游船最多使用量：（单位：艘）受当日客流量X（单位：万人）的限制，其关联关系如下表：
国庆节当日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
游船最多使用量 | 1 | 2 | 3 |
若某艘游船国庆节当日使用，则水面游览中心国庆节当日可获得利润3万元，若某艘游船国庆节当日不使用，则水面游览中心国庆节当日亏损0.5万元，记Y（单位：万元）表示该水面游览中心国庆节当日获得总利润，当Y的数学期望最大时称水面游览中心在国庆节当日效益最佳，问该水面游览中心的国庆节当日应投入多少艘游船才能使该水面游览中心在国庆节当日效益最佳？
