题目内容
【题目】抽样得到某次考试中高二年级某班8名学生的数学成绩和物理成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
(1) 求y与x的线性回归直线方程(系数保留到小数点后两位).
(2) 如果某学生的数学成绩为83分,预测他本次的物理成绩.
(参考公式:回归直线方程为![]() =
=![]() x+
x+![]() ,其中
,其中
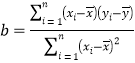 ,a=
,a=![]() -b
-b![]() .参考数据:
.参考数据:![]() =77.5,
=77.5,
![]() ≈84.9,
≈84.9,![]() ,
,![]() .)
.)
【答案】(1)![]() ;(2)89.
;(2)89.
【解析】
(1)先根据公式求![]() ,再根据求a=
,再根据求a=![]() -b
-b![]() 求a,(2)在回归直线方程中令x=83,解得y值,即为预测成绩.
求a,(2)在回归直线方程中令x=83,解得y值,即为预测成绩.
(1)从散点图可以看出,这些点分布在一条直线附近,因此可以用公式计算.
由![]() ,
,![]() ,
,
得 .
.
由![]() =77.5,
=77.5,![]() ≈84.9,
≈84.9,
得a=![]() -b
-b![]() ≈84.9-0.66×77.5=33.75,
≈84.9-0.66×77.5=33.75,
所以回归直线方程为![]() .
.
(2)当x=83时,
y=0.66×83+33.75
=88.53≈89.
因此某学生数学成绩为83分时,物理成绩约为89分.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()