题目内容
【题目】在△ABC中，内角A= 
，P为△ABC的外心，若 
=λ1 
+2λ2 
，其中λ1与λ2为实数，则λ1+λ2的最大值为（ ）
A.
B.1﹣ 
C.
D.1+ 
【答案】B
【解析】解：设|AB|=c，|AC|=b，
则： 
= 
c2 ， 
= b2；
又cosA= ，在 =λ1 +2λ2 的两边分别乘以 ， 得：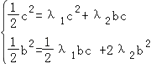 
；
整理得，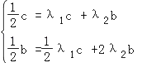 
，
解得，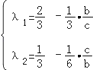 
；
∴λ1+λ2=1﹣（ 
+ 
）≤1﹣2 
=1﹣ 
；
∴λ1+λ2的最大值为 1﹣ ．
故选：B
【考点精析】解答此题的关键在于理解基本不等式的相关知识，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
，以及对平面向量的基本定理及其意义的理解，了解如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某风景区水面游览中心计划国庆节当日投入之多3艘游船供游客观光，过去10年的数据资料显示每年国庆节当日客流量X（单位：万人）都大于1，并把客流量分成三段整理得下表：
国庆节当日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
频数 | 2 | 4 | 4 |
以这10年的数据资料记录的隔断客流量的频率作为每年客流量在隔断发生的概率，且每年国庆节当日客流量相互独立．
（1）求未来连续3年国庆节当日中，恰好有1年国庆节当日客流量超过5万人的概率；
（2）该水面游览中心希望投入的游船尽可能使用，但每年国庆节当日游船最多使用量：（单位：艘）受当日客流量X（单位：万人）的限制，其关联关系如下表：
国庆节当日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
游船最多使用量 | 1 | 2 | 3 |
若某艘游船国庆节当日使用，则水面游览中心国庆节当日可获得利润3万元，若某艘游船国庆节当日不使用，则水面游览中心国庆节当日亏损0.5万元，记Y（单位：万元）表示该水面游览中心国庆节当日获得总利润，当Y的数学期望最大时称水面游览中心在国庆节当日效益最佳，问该水面游览中心的国庆节当日应投入多少艘游船才能使该水面游览中心在国庆节当日效益最佳？
