题目内容
已知点A(-1,0),B(1,-1)和抛物线.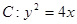 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(1)证明: 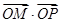 为定值;
为定值;
(2)若△POM的面积为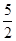 ,求向量
,求向量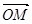 与
与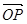 的夹角;
的夹角;
(3)证明直线PQ恒过一个定点.
(1)见解析; (2) 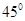 ;(3)直线PQ过定点E(1,-4).
;(3)直线PQ过定点E(1,-4).
解析试题分析:(1)设点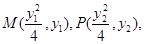 根据
根据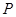 、M、A三点共线,
、M、A三点共线,
得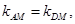
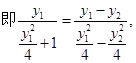 计算得到
计算得到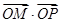 =5;
=5;
(2)设∠POM=α,可得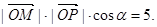 结合三角形面积公式可得tanα="1."
结合三角形面积公式可得tanα="1."
根据角的范围,即得所求.
(3)设点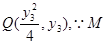 、B、Q三点共线,
、B、Q三点共线,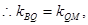
据此确定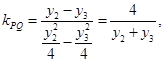 进一步确定
进一步确定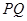 的方程,化简为
的方程,化简为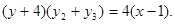
得出结论.
试题解析:(1)设点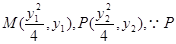 、M、A三点共线,
、M、A三点共线,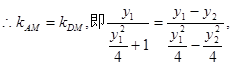
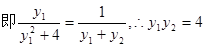 2分
2分 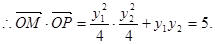 5分
5分
(2)设∠POM=α,则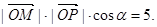
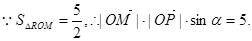 由此可得tanα=1. 8分
由此可得tanα=1. 8分
又 10分
10分
(3)设点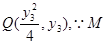 、B、Q三点共线,
、B、Q三点共线,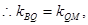
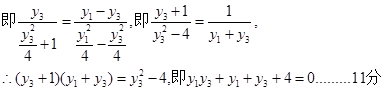
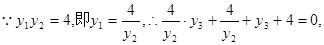
即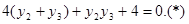 12分
12分 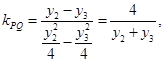
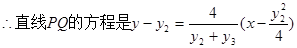
即 13分
13分
由(*)式,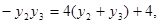 代入上式,得
代入上式,得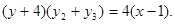
由此可知直线PQ过定点E(1,-4). 14分
考点:抛物线及其几何性质,直线方程,直线与抛物线的位置关系,转化与化归思想.

练习册系列答案
相关题目
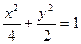 的左、右焦点分别为
的左、右焦点分别为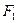 、
、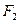 ,直线
,直线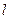 过
过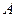 、
、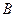 两点,
两点,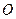 为坐标原点,以
为坐标原点,以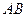 为直径的圆恰好过
为直径的圆恰好过 :
: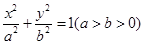 的左焦点
的左焦点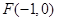 ,离心率为
,离心率为 ,函数
,函数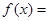
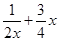 ,
, 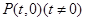 ,
,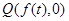 ,过
,过 的直线
的直线 交椭圆
交椭圆 两点,求
两点,求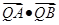 的最小值,并求此时的
的最小值,并求此时的 的值.
的值. 分别是椭圆
分别是椭圆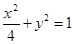 的左,右焦点.
的左,右焦点. 是椭圆在第一象限上一点,且
是椭圆在第一象限上一点,且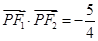 ,求
,求 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点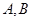 ,且
,且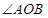 为锐角(其中
为锐角(其中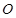 为原点),求直线
为原点),求直线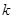 的取值范围.
的取值范围.
 的离心率为
的离心率为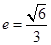 ,过
,过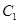 的左焦点
的左焦点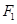 的直线
的直线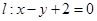 被圆
被圆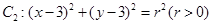 截得的弦长为
截得的弦长为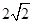 .
.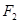 ,在圆
,在圆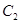 上是否存在点
上是否存在点 ,满足
,满足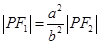 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.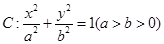 的两个焦点分别为
的两个焦点分别为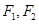 ,且
,且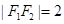 ,点
,点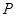 在椭圆上,且
在椭圆上,且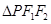 的周长为6.
的周长为6.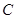 的方程;(2)若点
的方程;(2)若点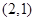 ,不过原点
,不过原点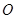 的直线
的直线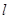 与椭圆
与椭圆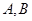 不同两点,设线段
不同两点,设线段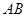 的中点为
的中点为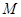 ,且
,且 三点共线.设点
三点共线.设点 ,求
,求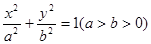 的右焦点为
的右焦点为 ,
, 为上顶点,
为上顶点, 为坐标原点,若△
为坐标原点,若△ 的面积为
的面积为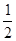 ,且椭圆的离心率为
,且椭圆的离心率为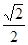 .
. 交椭圆于
交椭圆于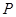 ,
, 两点, 且使点
两点, 且使点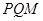 的垂心?若存在,求出直线
的垂心?若存在,求出直线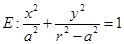 的焦点在
的焦点在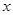 轴上,
轴上, 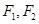 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点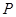 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线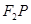 交
交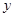 轴于点
轴于点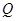 ,
, 时,
时,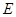 的离心率为
的离心率为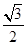 ,求椭圆
,求椭圆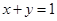 上时,求直线
上时,求直线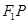 与
与 的夹角;
的夹角;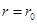 时,若总有
时,若总有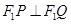 ,猜想:当
,猜想:当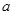 变化时,点
变化时,点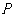 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).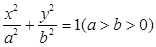 经过点
经过点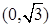 ,离心率为
,离心率为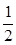 ,左右焦点分别为
,左右焦点分别为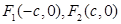 .
.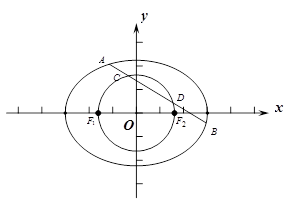
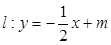 与椭圆交于
与椭圆交于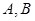 两点,与以
两点,与以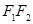 为直径的圆交于
为直径的圆交于 两点,且满足
两点,且满足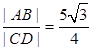 ,求直线
,求直线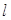 的方程.
的方程.