题目内容
【题目】某个地区计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水的年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过12的概率;
(2)若水的年入流量![]() 与其蕴含的能量
与其蕴含的能量![]() (单位:百亿万焦)之间的部分对应数据为如下表所示:
(单位:百亿万焦)之间的部分对应数据为如下表所示:
年入流量 | 6 | 8 | 10 | 12 | 14 |
蕴含的能量 | 1.5 | 2.5 | 3.5 | 5 | 7.5 |
用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(回归方程系数用分数表示)
;(回归方程系数用分数表示)
(3)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
附:回归方程系数公式: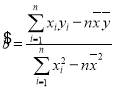 ,
,![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)欲使水电站年总利润的均值达到最大,应安装发电机2台.
(3)欲使水电站年总利润的均值达到最大,应安装发电机2台.
【解析】
(1)计算得到![]() ,
,![]() ,
,![]() ,再计算概率得到答案.
,再计算概率得到答案.
(2)利用回归方程公式直接计算得到答案.
(3)计算概率得到分布列,再计算数学期望得到答案.
(1)依题意,![]() ,
,![]() ,
,
![]() .
.
由二项分布得,在未来4年中至多有1年的年入流量超过12的概率为![]()
![]() .
.
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(3)记水电站年总利润为![]() (单位:万元).
(单位:万元).
①安装1台发电机的情形.
由于水库年入流量总大于4,故一台发电机运行的概率为1,对应的年利润![]() ,
,
![]() .
.
②安装2台发电机的情形.
依题意,当![]() 时,一台发电机运行,此时
时,一台发电机运行,此时![]() ,
,
因此![]() ;
;
当![]() 时,两台发电机运行,此时
时,两台发电机运行,此时![]() ,
,
因此![]() .由此得
.由此得![]() 的分布列如下:
的分布列如下:
| 4200 | 10000 |
| 0.2 | 0.8 |
所以,![]() .
.
③安装3台发电机的情形.
依题意,当![]() 时,一台发电机运行,此时
时,一台发电机运行,此时![]() ,
,
因此![]() ;
;
当![]() 时,两台发电机运行,此时
时,两台发电机运行,此时![]() ,
,
因此![]() ;
;
当![]() 时,三台发电机运行,此时
时,三台发电机运行,此时![]() ,
,
因此![]() .由此得
.由此得![]() 的分布列如下:
的分布列如下:
| 3400 | 9200 | 15000 |
| 0.2 | 0.7 | 0.1 |
所以,![]() .
.
综上,欲使水电站年总利润的均值达到最大,应安装发电机2台.

 高中必刷题系列答案
高中必刷题系列答案【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
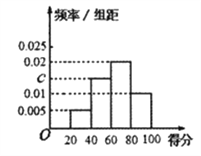
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?