题目内容
【题目】设![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是AB的垂直平分线,
是AB的垂直平分线,
(1)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(2)若![]() ,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
【答案】(1)![]() ,证明见解析 (2)过定点,(0,
,证明见解析 (2)过定点,(0,![]() )
)
【解析】
(1)对直线![]() 的斜率是否存在进行讨论,利用中垂线的性质列方程组求出直线的截距b的范围,从而得出结论;
的斜率是否存在进行讨论,利用中垂线的性质列方程组求出直线的截距b的范围,从而得出结论;
(2)设AB的方程为:y=kx+b,联立方程组,根据根与系数的关系和![]() 求出b的值,从而得到定点的坐标.
求出b的值,从而得到定点的坐标.
解:(1)∵抛物线![]() ,即
,即![]() ,
,
∴焦点为![]()
(i)直线![]() 的斜率不存在时,显然有
的斜率不存在时,显然有![]()
(ii)直线![]() 的斜率存在时,设为k,截距为b
的斜率存在时,设为k,截距为b
即直线![]() :y=kx+b,由已知得:
:y=kx+b,由已知得:
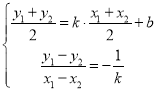
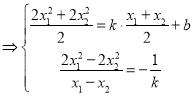
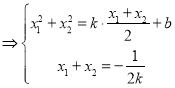
![]()
![]()
即![]() 的斜率存在时,不可能经过焦点
的斜率存在时,不可能经过焦点![]()
所以当且仅当![]() =0时,直线
=0时,直线![]() 经过抛物线的焦点F
经过抛物线的焦点F
(2)设直线![]() :y=kx+b,
:y=kx+b,
联立方程组:![]()
![]()
![]()
若![]() ,则
,则
过定点(0,![]() ).
). ![]() ,
,
![]()
![]()
因此直线AB过定点![]() .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
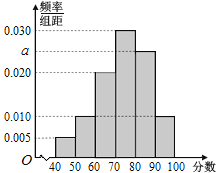
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某个地区计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水的年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过12的概率;
(2)若水的年入流量![]() 与其蕴含的能量
与其蕴含的能量![]() (单位:百亿万焦)之间的部分对应数据为如下表所示:
(单位:百亿万焦)之间的部分对应数据为如下表所示:
年入流量 | 6 | 8 | 10 | 12 | 14 |
蕴含的能量 | 1.5 | 2.5 | 3.5 | 5 | 7.5 |
用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(回归方程系数用分数表示)
;(回归方程系数用分数表示)
(3)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
附:回归方程系数公式: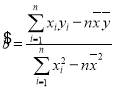 ,
,![]() .
.