题目内容
【题目】随着智能手机的发展，各种“APP”（英文单词Application的缩写，一般指手机软件）应运而生．某机构欲对A市居民手机内安装的APP的个数和用途进行调研，在使用智能手机的居民中随机抽取100人，获得了他们手机内安装APP的个数，整理得到如图所示频率分布直方图．
（Ⅰ）求a的值；
（Ⅱ）从被抽取安装APP的个数不低于50的居民中，随机抽取2人进一步调研，求这2人安装APP的个数都低于60的概率；
（Ⅲ）假设同组中的数据用该组区间的右端点值代替，以本次被抽取的居民情况为参考，试估计A市使用智能手机的居民手机内安装APP的平均个数在第几组（只需写出结论）．
【答案】（Ⅰ）a=0.025 （Ⅱ）
（Ⅲ）第4组（或者写成[30，40））．
【解析】
（Ⅰ）由频率分布直方图的性质，即可求得
的值，得到答案.
（Ⅱ）设事件A为“这2人手机内安装“APP”的数量都低于60”．被抽取的智能手机内安装“APP”的数量在[50，60）的有4人，分别记为a1，a2，a3，a4，被抽取的智能手机内安装“APP”的数量在[60，70]的有1人，记为b1，从被抽取的智能手机内安装“APP”的数量不低于50的居民中随机抽取2人进一步调研，利用列举法能求出这2人安装APP的个数都低于60的概率．
（Ⅲ）利用平均数的计算公式，即可求解A市使用智能手机的居民手机内安装APP的平均个数，得到答案．
（Ⅰ）由（0.011+0.016+a+a+0.018+0.004+0.001）
10=1，得
0.025．
（Ⅱ）设事件A为“这2人手机内安装“APP”的数量都低于60”
被抽取的智能手机内安装“APP”的数量在[50，60）的有0.004×10×100=4人，
分别记为a1，a2，a3，a4，
被抽取的智能手机内安装“APP”的数量在[60，70]的有0.001×10×100=1人，记为b1，
从被抽取的智能手机内安装“APP”的数量不低于50的居民中随机抽取2人进一步调研，
共包含10个基本事件，
分别为
，
，a1a4，a1b1，a2a3，a2a4，a2b1，a3a4，a3b1，a4b1，
事件A包含6个基本事件，
分别为
，，a1a4，a2a3，a2a4，a3a4，
则这2人安装APP的个数都低于60的概率
．
（Ⅲ）由题意，可得估计A市使用智能手机的居民手机内安装APP的平均个数为:
，
所以可得A市使用智能手机的居民手机内安装APP的平均个数位于第4组．
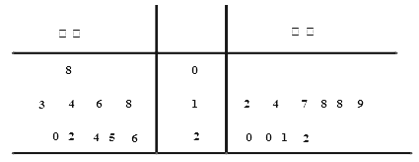
【题目】某个地区计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水的年入流量
（年入流量：一年内上游来水与库区降水之和，单位：十亿立方米）都在4以上，其中，不足8的年份有10年，不低于8且不超过12的年份有35年，超过12的年份有5年，将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多有1年的年入流量超过12的概率；
（2）若水的年入流量与其蕴含的能量
（单位：百亿万焦）之间的部分对应数据为如下表所示：
年入流量 | 6 | 8 | 10 | 12 | 14 |
蕴含的能量 | 1.5 | 2.5 | 3.5 | 5 | 7.5 |
用最小二乘法求出关于的线性回归方程
；（回归方程系数用分数表示）
（3）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系：
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
附：回归方程系数公式：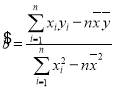
，
.
