Question

【题目】已知函数f（x）=x2+2ax+2，x∈[﹣5，5]．
（1）求实数a的范围，使y=f（x）在区间[﹣5，5]上是单调函数．
（2）求f（x）的最小值．

Answer 1

【答案】
（1）解：因为f（x）是开口向上的二次函数，且对称轴为x=﹣a，

为了使f（x）在[﹣5，5]上是单调函数，故﹣a≤﹣5或﹣a≥5，即a≥5或a≤﹣5

（2）解：①当﹣a≤﹣5，即a≥5时，f（x）在[﹣5，5]上是增函数，

所以fmin（x）=f（﹣5）=27﹣10a

②当﹣5＜﹣a≤5，即﹣5≤a＜5时，f（x）在[﹣5，﹣a]上是减函数，在[﹣a，5]上是增函数，

所以

③当﹣a＞5，即a＜﹣5时，f（x）在[﹣5，5]上是减函数，

所以fmin（x）=f（5）=27+10a

综上可得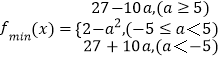

【解析】（1）由题意，得函数y=f（x）的单调区间是（﹣∞，﹣a]，[﹣a，+∞），
由于y=f（x）在区间[﹣5，5]上是单调函数故﹣a≤﹣5或﹣a≥5，即可得到实数a的取值范围；（2）分类讨论，得到函数在[﹣5，5]上的增减性，继而得到函数在[﹣5，5]上的最小值．
【考点精析】本题主要考查了二次函数在闭区间上的最值的相关知识点，需要掌握当时，当时，；当时在上递减，当时，才能正确解答此题．