题目内容
【题目】设函数 
的定义域为A，函数y=log2（a﹣x）的定义域为B．
（1）若AB，求实数a的取值范围；
（2）设全集为R，若非空集合（RB）∩A的元素中有且只有一个是整数，求实数a的取值范围．
【答案】
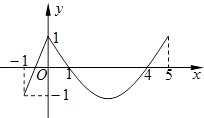
（1）解：由 
，
∴A=[﹣1，2]
由a﹣x＞0得x＜a，
∴B=（﹣∞，a）．
∵AB，
∴a＞2
（2）解：∵B=（﹣∞，a），
∴RB=[a，+∞）．
∵（RB）∩A的元素中有且只有一个是整数，
∴1＜a≤2
【解析】（1）根据函数的定义域求法求出A，B，然后利用AB，即可求实数a的取值范围；（2）求出RB，利用非空集合（RB）∩A的元素中有且只有一个是整数，即可求实数a的取值范围．
【考点精析】解答此题的关键在于理解对数函数的定义域的相关知识，掌握对数函数的定义域范围:（0，+∞）．
练习册系列答案
阅读快车系列答案
相关题目
