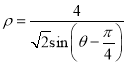ЬтФПФкШн
ЁОЬтФПЁПФГФъМЖОйАьЭХжЊЪЖОКШќ.![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФИіАрБЈУћШЫЪ§ШчЯТЃК
ЫФИіАрБЈУћШЫЪ§ШчЯТЃК
АрБ№ |
|
|
|
|
ШЫЪ§ | 45 | 60 | 30 | 15 |
ФъМЖдкБЈУћЕФЭЌбЇжаАДЗжВуГщбљЕФЗНЪНГщШЁ10УћЭЌбЇВЮМгОКШќЃЌУПЮЛВЮМгОКШќЕФЭЌбЇДг10ИіЙигкЭХжЊЪЖЕФЬтФПжаЫцЛњГщШЁ4ИізїД№ЃЌШЋВПД№ЖдЕФЭЌбЇЛёЕУвЛЗнНБЦЗ.
ЃЈЂёЃЉЧѓИїАрВЮМгОКШќЕФШЫЪ§ЃЛ
ЃЈЂђЃЉШє![]() АрУПЮЛВЮМгОКШќЕФЭЌбЇЖдУПИіЬтФПД№ЖдЕФИХТЪОљЮЊ
АрУПЮЛВЮМгОКШќЕФЭЌбЇЖдУПИіЬтФПД№ЖдЕФИХТЪОљЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() АрЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЃЛ
АрЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЃЛ
ЃЈЂѓЃЉШєет10ИіЬтФПЃЌаЁеХЭЌбЇжЛга2ИіД№ВЛЖдЃЌМЧаЁеХД№ЖдЕФЬтФПЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ
ЕФЗжВМСаМАЪ§бЇЦкЭћ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉгЩЗжВуГщбљЕФИХФюПЩЕУ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФИіАрВЮМгОКШќЕФШЫЪ§ЃЛЃЈЂђЃЉЯШМЦЫуГі
ЫФИіАрВЮМгОКШќЕФШЫЪ§ЃЛЃЈЂђЃЉЯШМЦЫуГі![]() АржаУПЮЛВЮМгОКШќЕФЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ
АржаУПЮЛВЮМгОКШќЕФЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ![]() ЃЌЙЪ
ЃЌЙЪ![]() АржаЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ
АржаЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ![]() ЃЛЃЈЂѓЃЉгЩЬтвтПЩЕУЃК
ЃЛЃЈЂѓЃЉгЩЬтвтПЩЕУЃК![]() ЕФШЁжЕЮЊ2ЃЌ3ЃЌ4ЃЎ
ЕФШЁжЕЮЊ2ЃЌ3ЃЌ4ЃЎ![]() ЗўДгГЌМИКЮЗжВМЃЌМДПЩЕУГі.
ЗўДгГЌМИКЮЗжВМЃЌМДПЩЕУГі.
ЪдЬтНтЮіЃКЃЈЂёЃЉ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФИіАрВЮМгОКШќЕФШЫЪ§ЗжБ№ЮЊЃК
ЫФИіАрВЮМгОКШќЕФШЫЪ§ЗжБ№ЮЊЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈЂђЃЉИљОнЬтвтЃЌ![]() АржаУПЮЛВЮМгОКШќЕФЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ
АржаУПЮЛВЮМгОКШќЕФЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() АржаЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ
АржаЧЁКУга2ЮЛЭЌбЇЛёЕУНБЦЗЕФИХТЪЮЊ![]()
![]() .
.
ЃЈЂѓЃЉгЩЬтвтЃЌ![]() ШЁжЕЮЊ2ЃЌ3ЃЌ4ЃЌЗўДгГЌМИКЮЗжВМ.
ШЁжЕЮЊ2ЃЌ3ЃЌ4ЃЌЗўДгГЌМИКЮЗжВМ.
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
Ыљвд![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 2 | 3 | 4 |
|
|
|
|
Ыљвд![]()
![]() .
.

ЁОЬтФПЁПФГбаОПадбЇЯАаЁзщЖдДКМОжчвЙЮТВюДѓаЁгыФГЛЈЛмжжзгЗЂбПЖрЩйжЎМфЕФЙиЯЕНјаабаОПЃЌЫћУЧЗжБ№МЧТМСЫ3дТ1ШежС3дТ5ШеЕФУПЬьжчвЙЮТВюгыЪЕбщЪвУПЬь100ПХжжзгНўХнКѓЕФЗЂбПЪ§ЃЌЕУЕНШчЯТзЪСЯЃК
KШе ШеЦкЦк | 1Ше | 2Ше | 3Ше | 4Ше | 5Ше |
ЮТВюx(Ёц) | 10 | 11 | 13 | 12 | 8 |
ЗЂбПЪ§y(ПХ) | 23 | 25 | 30 | 26 | 16 |
(1)Чѓет5ЬьЗЂбПЪ§ЕФжаЮЛЪ§ЃЛ
(2)Чѓет5ЬьЕФЦНОљЗЂбПТЪЃЛ
(3)Дг3дТ1ШежС3дТ5ШежаШЮбЁ2ЬьЃЌМЧЧАУцвЛЬьЗЂбПЕФжжзгЪ§ЮЊmЃЌКѓУцвЛЬьЗЂбПЕФжжзгЪ§ЮЊnЃЌгУ(mЃЌn)ЕФаЮЪНСаГіЫљгаЛљБОЪТМўЃЌВЂЧѓТњзуЁА![]() ЁБЕФИХТЪЃЎ
ЁБЕФИХТЪЃЎ