题目内容
已知函数f(x)=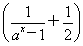 x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
(1){x|x∈R,且x≠0}(2)偶函数(3)a>1.
【解析】(1)由于ax-1≠0,则ax≠1,所以x≠0,
所以函数f(x)的定义域为{x|x∈R,且x≠0}.
(2)对于定义域内任意的x,有
f(-x)=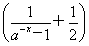 (-x)3=-
(-x)3=-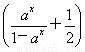 x3=-
x3=- x3=
x3=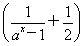 x3=f(x)所以f(x)是偶函数.
x3=f(x)所以f(x)是偶函数.
(3)①当a>1时,对x>0,
所以ax>1,即ax-1>0,所以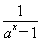 +
+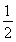 >0.
>0.
又x>0时,x3>0,所以x3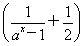 >0,
>0,
即当x>0时,f(x)>0.
由(2)知,f(x)是偶函数,即f(-x)=f(x),
则当x<0时,-x>0,有f(-x)=f(x)>0成立.
综上可知,当a>1时,f(x)>0在定义域上恒成立.
②当0<a<1时,f(x)=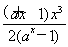 ,
,
当x>0时,0<ax<1,此时f(x)<0,不满足题意;
当x<0时,-x>0,有f(-x)=f(x)<0,也不满足题意.
综上可知,所求a的取值范围是a>1

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目