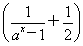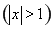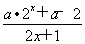题目内容
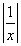
已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=-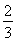 .
.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
(1)见解析(2)见解析(3)最大值为2,最小值为-4
【解析】(1)证明:令x=y=0,可得f(0)+f(0)=f(0+0),从而f(0)=0.令y=-x,可得f(x)+f(-x)=f(x-x)=0,即f(-x)=-f(x),故f(x)为奇函数.
(2)证明:设x1、x2∈R,且x1>x2,则x1-x2>0,于是f(x1-x2)<0.从而f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)+f(x2)-f(x2)=f(x1-x2)<0.所以f(x)为减函数.
(3)【解析】
由(2)知,所求函数的最大值为f(-3),最小值为f(6).f(-3)=-f(3)=-[f(2)+f(1)]=-2f(1)-f(1)=-3f(1)=2,f(6)=-f(-6)=-[f(-3)+f(-3)]=-4.于是f(x)在[-3,6]上的最大值为2,最小值为-4

练习册系列答案
相关题目