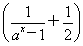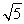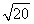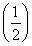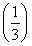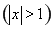题目内容
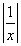
设函数f(x)=x2-1,对任意x∈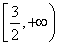 ,f
,f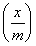 -4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.
-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.
m≤-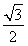 或m≥
或m≥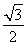
【解析】由题意知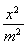 -1-4m2(x2-1)≤(x-1)2-1+4(m2-1)在x∈
-1-4m2(x2-1)≤(x-1)2-1+4(m2-1)在x∈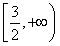 上恒成立,
上恒成立,
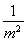 -4m2≤-
-4m2≤-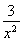 -
-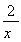 +1在x∈
+1在x∈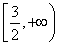 上恒成立,当x=
上恒成立,当x=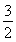 时,函数y=-
时,函数y=-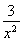 -
-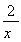 +1取得最小值-
+1取得最小值-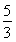 ,所以
,所以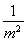 -4m2≤-
-4m2≤-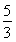 ,即(3m2+1)(4m2-3)≥0,
,即(3m2+1)(4m2-3)≥0,
解得m≤-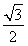 或m≥
或m≥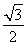 .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目