Question

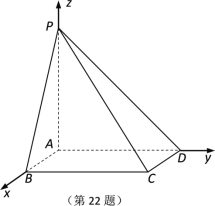
【题目】如图，三棱锥DABC中，已知AC⊥BC，AC⊥DC，BC＝DC，E，F分别为BD，CD的中点．求证：

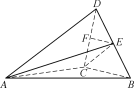
(1) EF∥平面ABC；

(2) BD⊥平面ACE.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据题意证出EF∥BC，再由线面平行的判定定理即可证出.

（2）首先证出AC⊥BD，CE⊥BD，利用线面垂直的判定定理即可证出.

(1)

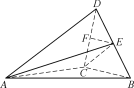
三棱锥DABC中，因为E为DB的中点，F为DC的中点，所以EF∥BC，

因为BC平面ABC，EF平面ABC，

所以EF∥平面ABC.

(2)因为AC⊥BC，AC⊥DC，BC∩DC＝C，BC，DC平面BCD

所以AC⊥平面BCD，

因为BD平面BCD，所以AC⊥BD，

因为DC＝BC，E为BD的中点，所以CE⊥BD，

因为ACCE＝C，AC，CE平面ACE，所以BD⊥平面ACE.