题目内容
【题目】已知函数![]() 部分图象如图所示.
部分图象如图所示.
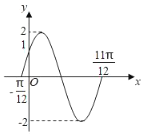
(1)求函数![]() 的解析式及
的解析式及![]() 的单调递增区间;
的单调递增区间;
(2)把函数![]() 图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 上所有的实数根之和.
上所有的实数根之和.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)先根据函数的周期求出![]() 的值,再利用点
的值,再利用点![]() 在函数图象上求出
在函数图象上求出![]() 的值,再根据点
的值,再根据点![]() 在函数图象上求出A的值得函数
在函数图象上求出A的值得函数![]() 的解析式,再求出
的解析式,再求出![]() 的单调递增区间;(2)先求出
的单调递增区间;(2)先求出![]() ,再利用三角函数的图象和性质分析得解.
,再利用三角函数的图象和性质分析得解.
(1)由题中图象知,最小正周期![]() ,
,![]() .
.
![]() 点
点![]() 在函数图象上,
在函数图象上,![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,![]() ,从而
,从而![]() .
.
又![]() 点
点![]() 在函数图象上,
在函数图象上,![]() ,
,![]() .
.
故函数![]() 的解析式为
的解析式为![]() .
.
令![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
故![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;
;
(2)依题意得![]() .
.
![]() 的最小正周期
的最小正周期![]() ,
,
![]() 在
在![]() 内有2个周期.
内有2个周期.
令![]() ,得
,得![]() ,
,
即函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() .
.
由![]() ,得
,得![]() .
.
又![]() ,
,
![]() 在
在![]() 内有4个实数根.
内有4个实数根.
将实数根从小到大依次设为![]() ,
,
则![]() ,
,![]() .
.
![]() 关于x的方程
关于x的方程![]() 在
在![]() 上所有的实数根之和为
上所有的实数根之和为![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,通过分层抽样获得部分员工每天睡眼的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | |||
乙部门 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 |
丙部门 | 5 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数?
(2)若将每天睡眠时间不少于7小时视为睡眠充足,现从该单位任取1人,估计拍到的此人为睡眠充足者的概率;
(3)再从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B,假设所有员工睡眠的时间相互独立,求A的睡眠时间不少于B的睡眼时间的概率.
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求至少有一人年龄在
人,求至少有一人年龄在![]() 岁以下的概率.
岁以下的概率.
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.


