题目内容
10.已知AB是⊙O的弦,P是AB上一点,AB=6$\sqrt{2},PA=4\sqrt{2}$,OP=3,求⊙O的半径R.
分析 过点O作OC⊥AB,交AB于点C,连结OA,由垂径定理和勾股定理求出OC⊥AB,PC=PA-AC=$\sqrt{2}$,OC=$\sqrt{7}$,由此能求出⊙O的半径R.
解答 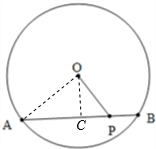 解:过点O作OC⊥AB,交AB于点C,连结OA
解:过点O作OC⊥AB,交AB于点C,连结OA
∵AB是⊙O的弦,P是AB上一点,AB=6$\sqrt{2},PA=4\sqrt{2}$,OP=3,
∴OC⊥AB,PC=PA-AC=4$\sqrt{2}$-3$\sqrt{2}$=$\sqrt{2}$,
∴OC=$\sqrt{O{P}^{2}-P{C}^{2}}$=$\sqrt{9-2}$=$\sqrt{7}$,
∴R=OA=$\sqrt{O{C}^{2}+A{C}^{2}}$=$\sqrt{7+18}$=5.
点评 本题考查圆的半径的求法,考查垂径定理和勾股定理的运用,是中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2.在△ABC中,内角A、B、C的对边分别是a,b,c,若sin2A+sin2B-sin2C=0,a2+c2-b2-ac=0,c=2,则a=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
1.sin80°cos20°-cos80°sin20°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
2.已知动点P与平面上两定点A(-$\sqrt{2}$,0),B($\sqrt{2}$,0)连线的斜率的积为定值-$\frac{1}{2}$.则动点P的轨迹方程C( )
| A. | $\frac{{x}^{2}}{5}$$+\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{2}$+y2=1 | C. | $\frac{{x}^{2}}{16}$$+\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$$+\frac{{y}^{2}}{9}$=1 |
20.已知集合A={0,b},B={x∈Z|x2-3x<0},若A∩B≠∅,则b等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |