题目内容
1.sin80°cos20°-cos80°sin20°的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由条件利用两角和的正弦公式,求得所给式子的值.
解答 解:sin80°cos20°-cos80°sin20°=sin(80°-20°)=sin60°=$\frac{\sqrt{3}}{2}$,
故选:B.
点评 主要考查两角和的正弦公式的应用,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.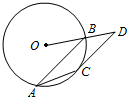 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
 如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )
如图,AB是半径为2的圆O的弦,CD是圆O的切线,C是切点,D是OB的延长线与CD的交点,CD∥AB,若CD=$\sqrt{5}$,则AC等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | 1 | D. | 2 |
9.若复数$\frac{a+i}{b-3i}$(a,b∈R)对应的点在虚轴上,则ab的值是( )
| A. | -15 | B. | 3 | C. | -3 | D. | 15 |
16.抛物线y=-$\frac{1}{8}{x^2}$的焦点坐标是( )
| A. | (0,$\frac{1}{32}$) | B. | ($\frac{1}{32}$,0) | C. | (0,-2) | D. | (-2,0) |
13.已知正三棱锥P-ABC,M和N分别为AB、PA的中点,MN⊥CN,若PA=1,则此正三棱锥的外接球表面积为( )
| A. | 5π | B. | 4π | C. | 3π | D. | 2π |
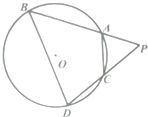 如图,过圆O外一点P引圆的两条割线分别交圆O于A、B、C、D四点.
如图,过圆O外一点P引圆的两条割线分别交圆O于A、B、C、D四点.