题目内容
13.若函数f(x)=$\frac{sinxcosx}{2co{s}^{2}x-1}$+$\frac{tanx}{1-ta{n}^{2}x}$,则f($\frac{π}{12}$)=$\frac{\sqrt{3}}{3}$.分析 利用三角函数的倍角公式进行化简即可.
解答 解:f(x)=$\frac{sinxcosx}{2co{s}^{2}x-1}$+$\frac{tanx}{1-ta{n}^{2}x}$=$\frac{\frac{1}{2}sin2x}{cos2x}$+$\frac{1}{2}$tan2x=$\frac{1}{2}$tan2x+$\frac{1}{2}$tan2x=tan2x,
则f($\frac{π}{12}$)=tan(2×$\frac{π}{12}$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题主要考查三角函数值的求解,利用三角函数的倍角公式是解决本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
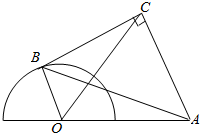 为改善居民的生活环境,政府拟将一公园进行改造扩建,已知原公园是直径为200米的半圆形,出入口在圆心O处,A为居民小区,OA的距离为200米,按照设计要求,以居民小区A和圆弧上点B为线段向半圆外作等腰直角三角形ABC(C为直角顶点),使改造后的公园成四边形OACB,如图所示.
为改善居民的生活环境,政府拟将一公园进行改造扩建,已知原公园是直径为200米的半圆形,出入口在圆心O处,A为居民小区,OA的距离为200米,按照设计要求,以居民小区A和圆弧上点B为线段向半圆外作等腰直角三角形ABC(C为直角顶点),使改造后的公园成四边形OACB,如图所示.