题目内容
1.设G为△ABC的重心,若AB=3,$\overrightarrow{AG}$•$\overrightarrow{AB}$=5,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=6.分析 运用三角形的重心的性质和向量的三角形法则及向量的中点表示,以及向量的平方即为模的平方,即可化简求得.
解答 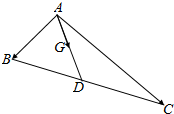 解:由于G为△ABC的重心,
解:由于G为△ABC的重心,
连接AG,延长交BC于D,
则$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
则有$\overrightarrow{AG}$•$\overrightarrow{AB}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AB}$
=$\frac{1}{3}$($\overrightarrow{AB}$2+$\overrightarrow{AB}$•$\overrightarrow{AC}$)
=$\frac{1}{3}$(9-$\overrightarrow{AB}$•$\overrightarrow{AC}$)=5.
可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=9-15=-6.
故答案为:-6.
点评 本题考查平面向量的数量积的定义和性质,考查三角形的重心的性质及向量中点的向量表示,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知两点A(-1,3),B(4,2),以AB为直径的圆与x轴相交于点C,则以AB为直径的圆与x轴相交于点C,则交点C的坐标是( )
| A. | (1,0) | B. | (2,0) | C. | (-1,0)或(2,0) | D. | (1,0)或(2,0) |
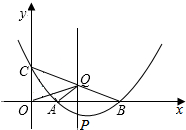 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.