题目内容
【题目】已知函数![]() .
.
(1)若![]() 的图像在
的图像在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 内单调递增,求实数
内单调递增,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极大值![]() ,无极小值;(2)
,无极小值;(2)![]() .
.
【解析】试题分析:(1)求出![]() ,由
,由![]() 求得
求得![]() ,研究函数的单调性,即可求得
,研究函数的单调性,即可求得![]() 的极值;(2)化简
的极值;(2)化简![]() ,可得
,可得![]() ,对求实数
,对求实数![]() 分三种情况
分三种情况![]() 讨论,分别利用导数研究函数的单调性,验证函数
讨论,分别利用导数研究函数的单调性,验证函数![]() 在
在![]() 内是否单调递增即可得结果.
内是否单调递增即可得结果.
试题解析:(1)因为![]() ,所以
,所以![]() .
.
由条件可得![]() ,解之得
,解之得![]() ,所以
,所以![]() ,
,
![]()
![]() .
.
令![]() 可得
可得![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
故![]() 有极大值
有极大值![]() ,无极小值;
,无极小值;
(2)![]() ,则
,则![]()
![]() .
.
设![]() ,
,
①当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,不满足条件;
内单调递减,不满足条件;
②当![]() 时,
时, ![]() 是开口向下的抛物线,方程
是开口向下的抛物线,方程![]() 有两个实根,设较大实根为
有两个实根,设较大实根为![]() .当
.当![]() 时,有
时,有![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 内单调递减,故不符合条件;
内单调递减,故不符合条件;
③当![]() 时,由
时,由![]() 可得
可得![]() 在
在![]() 内恒成立,
内恒成立,
故只需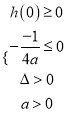 或
或![]() ,即
,即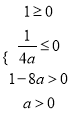 或
或![]() ,解之得
,解之得![]() .
.
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
画出上表数据的散点图如图所示
(其中  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力
