题目内容

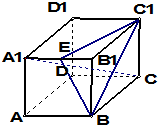在正方体ABCD-A1B1C1D1中，点E是棱A1B1的中点，
（1）求证：A1C∥面BEC1．
（2）求异面直线A1C与B1C1所成的角的正切值．
考点：异面直线及其所成的角,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连接B1C，交BC1与O，只要证明OE∥A1C即可；
（2）由正方体的性质可得异面直线A1C与B1C1所成的角为∠BCA1，再利用直角三角形的三角函数求正切．
解答： 证明：连接B1C，交BC1与O，如图

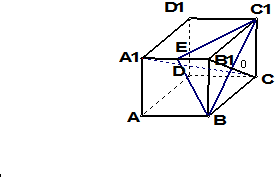
因为几何体是正方体，所以O是B1C的中点，又点E是棱A1B1的中点，所以OE∥A1C，因为OE?平面BEC1，A1C?平面BEC1，
所以A1C∥面BEC1．
（2）因为BC∥B1C1，所以异面直线A1C与B1C1所成的角为∠BCA1，
因为几何体是正方体，所以BC⊥A1B，
所以tan∠BCA1=
A1B
BC
=
2
．
点评：本题考查了以正方体为载体的线面平行的判定和异面直线所成的角的求法，关键是将所求转化为线线关系和平面角解答．
练习册系列答案
相关题目
求函数y=cos（2x+
π
3
）图象的一个对称中心．
已知函数f（x）=x-alnx（a∈R）
（1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性与极值；
（3）当a=2时，求函数f（x）在[1，3]上的最值．
在数列{an}中，a1=1，a1=1，an+1=（1+
1
n
）an+
n+1
2n

（Ⅰ）设bn=
an
n
，求数列{bn}的通项公式；
（Ⅱ）求数列{an}的前n项和Sn；
（Ⅲ）设cn=(2n-an)2n，求证：
1
c1c2
+
1
c2c3
+…+
1
cncn+1
＜
1
4
．
如图，椭圆与双曲线有公共焦点F1、F2，它们在第一象限的交点为A，且AF1⊥AF2，∠AF1F2=30°，则椭圆与双曲线的离心率的倒数和为（　　）
A、2
3
B、
3
C、2
D、1
一个正整数数表如（表中下一行中的数的个数比上一行中数的个数多一个），则第7行中的第2个数是（　　）
第1行1
第2行2   3
第3行4   5   6  
……
A、24B、23C、22D、21
已知元素为正整数的数集序列{1}，{2，3}，{4，5，6}，{7，8，9，10}，…从第二个数集开始，每一个数集比前一个数集多一个元素，且每一个数集中最小的元素比前一个数集中最大的元素大1，则第n个数集中所有元素之和Sn=
 
．
已知偶函数f（x）满足f（x+1）=f（x-1），且当x∈[0，1]时，f（x）=x2，则关于x的方程f（x）=2-2|x|
在[-5，5]上根的个数是（　　）
A、4个B、6个C、8个D、10个
已知双曲线
x2
a2
-
y2
b2
=1的一条渐近线方程为y=
4
3
x，则双曲线的离心率为（　　）
A、
5
4
B、
5
3
C、
3
4
D、
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网