题目内容
如图,在四棱锥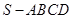 中,
中,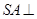 平面
平面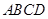 ,底面
,底面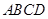 为直角梯形,
为直角梯形,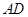 ∥
∥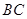 ,
,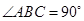 ,
,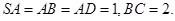
(Ⅰ)求异面直线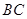 与
与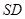 所成角的大小;
所成角的大小;
(Ⅱ)求直线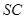 与平面
与平面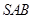 所成角的正切值;
所成角的正切值;
(Ⅲ)求三棱锥 的体积.
的体积.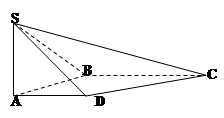
 中,
中, 平面
平面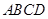 ,底面
,底面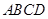 为直角梯形,
为直角梯形,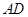 ∥
∥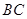 ,
,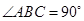 ,
,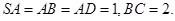
(Ⅰ)求异面直线
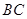 与
与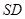 所成角的大小;
所成角的大小;(Ⅱ)求直线
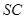 与平面
与平面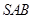 所成角的正切值;
所成角的正切值;(Ⅲ)求三棱锥
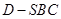 的体积.
的体积.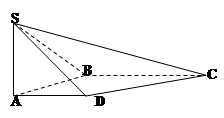
(1)45o;;(2)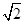 ;(3)
;(3)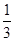 .
.
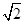 ;(3)
;(3)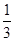 .
.本试题主要是考查了空间中四棱锥中异面直线所成的角,以及线面角的求解和棱锥的体积的综合运用试题。可以建立直角坐标系,向量法来解,也可以运用几何性质来求解。
解:(Ⅰ)∵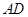 ∥
∥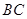
 异面直线
异面直线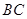 与
与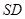 所成角是∠SDA或其补角
所成角是∠SDA或其补角
∵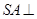 平面
平面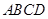 ,
, 平面
平面

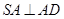 在Rt△SAD中, ∵
在Rt△SAD中, ∵ ,
,
 ∠SDA=45o
∠SDA=45o
 异面直线
异面直线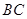 与
与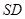 所成角的大小为45o.
所成角的大小为45o.
(Ⅱ) 又∵
又∵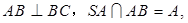
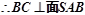

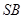 是
是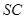 在平面
在平面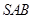 上的射影,
上的射影, ∠CSB是
∠CSB是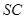 与底面
与底面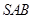 所成角
所成角
在Rt△CSB中tan∠CSB=

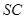 与底面
与底面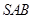 所成角的正切值为
所成角的正切值为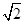
(Ⅲ)
解:(Ⅰ)∵
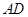 ∥
∥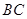
 异面直线
异面直线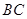 与
与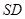 所成角是∠SDA或其补角
所成角是∠SDA或其补角∵
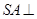 平面
平面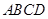 ,
, 平面
平面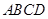

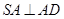 在Rt△SAD中, ∵
在Rt△SAD中, ∵ ,
,
 ∠SDA=45o
∠SDA=45o 异面直线
异面直线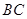 与
与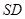 所成角的大小为45o.
所成角的大小为45o.(Ⅱ)
 又∵
又∵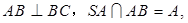
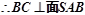

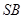 是
是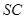 在平面
在平面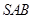 上的射影,
上的射影, ∠CSB是
∠CSB是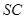 与底面
与底面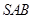 所成角
所成角 在Rt△CSB中tan∠CSB=


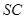 与底面
与底面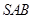 所成角的正切值为
所成角的正切值为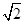
(Ⅲ)


练习册系列答案
相关题目
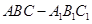 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
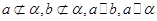 。求证:
。求证: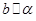 。
。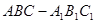 中,点
中,点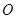 、
、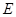 分别是
分别是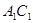 、
、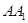 的中点,
的中点,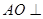 平面
平面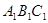 .已知
.已知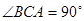 ,
,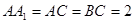 .
.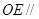 平面
平面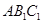 ;
;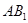 与
与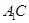 所成的角;
所成的角; 所成角的正弦值.
所成角的正弦值.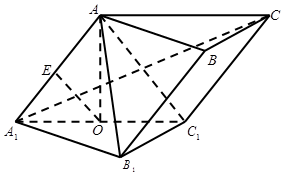
 、
、 、
、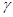 和直线
和直线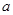 、
、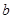 、
、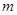 、
、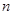 ,下列命题中真命题是( )
,下列命题中真命题是( )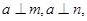
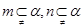 ,则
,则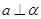 ;
;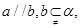 则
则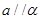 ;
;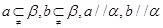 ,则
,则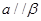 ;
;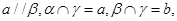 则
则 .
.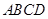 的对角线
的对角线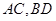 交于点
交于点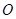 ,
,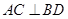 ,且
,且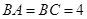 ,
,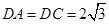 ,
,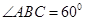 .现沿对角线
.现沿对角线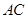 将三角形
将三角形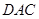 翻折,使得平面
翻折,使得平面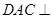 平面
平面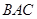 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: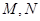 分别为
分别为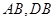 的中点.①求二面角
的中点.①求二面角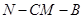 大小的余弦值; ②求点
大小的余弦值; ②求点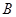 到平面
到平面 的距离
的距离 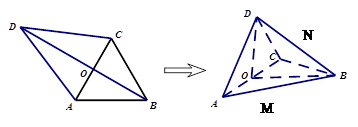
 A
A AOB和
AOB和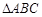 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,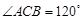 ,现将
,现将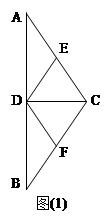
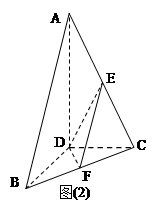
 DE?证明你的结论.
DE?证明你的结论. 是平面,
是平面,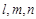 是直线,则下列命题正确的是( )
是直线,则下列命题正确的是( )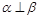 ,
,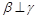 ,则
,则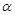 ∥
∥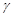
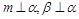 ,则
,则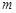 ∥
∥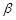
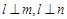 ,则
,则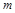 ∥
∥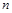
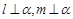 ,则
,则 ∥
∥