题目内容
2.在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的一个顶点为A(-2,0),离心率为$\frac{{\sqrt{6}}}{3}$.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)直线l过点A,过O作l的平行线交椭圆C于P,Q两点,如果以PQ为直径的圆与直线l相切,求l的方程.
分析 (Ⅰ)利用椭圆的焦点在x轴上,a=2,$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,计算即得结论;
(Ⅱ)通过设直线l的方程,利用以PQ为直径的圆与直线l相切,即$\frac{1}{2}$|PQ|与原点O到直线l的距离相等,计算即可.
解答 解:(Ⅰ)依题意,椭圆的焦点在x轴上,
∵a=2,$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,
∴c=$\frac{2\sqrt{6}}{3}$,b2=a2-c2=$\frac{4}{3}$,
∴椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{3{y}^{2}}{4}$=1;
(Ⅱ)依题意,直线l的斜率显然存在且不为0,设l的斜率为k,
则可设直线l的方程为:y=k(x+2),
则原点O到直线l的距离d=$\frac{|2k|}{\sqrt{1+{k}^{2}}}$.
设P(x1,y1),Q(x2,y2),
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+3{y}^{2}=4}\end{array}\right.$,消去y整理得:(1+3k2)x2=4,
可得P($\frac{2}{\sqrt{1+3{k}^{2}}}$,$\frac{2k}{\sqrt{1+3{k}^{2}}}$),Q(-$\frac{2}{\sqrt{1+3{k}^{2}}}$,-$\frac{2k}{\sqrt{1+3{k}^{2}}}$),
∵以PQ为直径的圆与直线l相切,
∴$\frac{1}{2}$|PQ|=d,即|OP|=d,
∴($\frac{2}{\sqrt{1+3{k}^{2}}}$)2+($\frac{2k}{\sqrt{1+3{k}^{2}}}$)2=($\frac{|2k|}{\sqrt{1+{k}^{2}}}$)2,
解得:k=±1,
∴直线l的方程为x-y+2=0或x+y+2=0.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
 如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.
如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.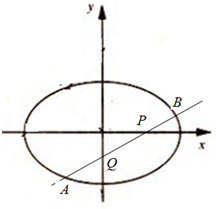 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.