题目内容
4.设函数f(x)=3sin($\frac{1}{2}$x-$\frac{π}{6}$),则该函数的振幅为3,最小正周期为4π.分析 由条件根据主要考查函数y=Asin(ωx+φ)的振幅和周期,得出结论.
解答 解:对于函数f(x)=3sin($\frac{1}{2}$x-$\frac{π}{6}$),它的振幅为3,最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,
故答案为:3;4π.
点评 本题主要考查函数y=Asin(ωx+φ)的振幅和周期,属于基础题.

练习册系列答案
相关题目
15.若x∈[0,2π],则sinx+cosx<1的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
12.一个四棱锥的侧棱长都相等,底面是正方形,其主视图如图所示,该四棱锥侧面积等于( )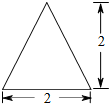

| A. | 20 | B. | 5$\sqrt{2}$ | C. | 4($\sqrt{5}$+1) | D. | 4$\sqrt{5}$ |
19.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{b}$|=2,$\overrightarrow{b}$$•(2\overrightarrow{a}-\overrightarrow{b})$=0,则|$\overrightarrow{a}$|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
16.已知α∈(π,2π),且cosα+sinα=$\frac{1}{5}$,则tanα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
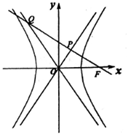 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.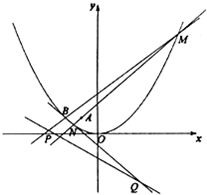 (Ⅰ)求抛物线C的方程;
(Ⅰ)求抛物线C的方程;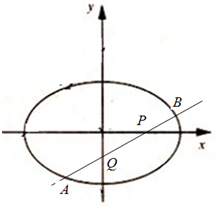 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.