题目内容
19.设常数a>1,实数x,y满足logax+2logxa+logxy=-3,若y的最大值为$\sqrt{2}$,则x的值为$\frac{1}{8}$.分析 实数x,y满足logax+2logxa+logxy=-3,化为logax+$\frac{2}{lo{g}_{a}x}$+$\frac{lo{g}_{a}y}{lo{g}_{a}x}$=-3,令logax=t,化为:logay=$-(t+\frac{3}{2})^{2}$+$\frac{1}{4}$,再利用二次函数的单调性、对数的运算性质即可得出.
解答 解:实数x,y满足logax+2logxa+logxy=-3,
化为logax+$\frac{2}{lo{g}_{a}x}$+$\frac{lo{g}_{a}y}{lo{g}_{a}x}$=-3,
令logax=t,
化为:logay=$-(t+\frac{3}{2})^{2}$+$\frac{1}{4}$,
∵a>1,∴当t=-$\frac{3}{2}$时,y取得最大值$\sqrt{2}$,
∴$lo{g}_{a}\sqrt{2}$=$\frac{1}{4}$,
解得a=4.
∴log4x=-$\frac{3}{2}$,
∴x=${4}^{-\frac{3}{2}}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查了二次函数的单调性、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.一个四棱锥的侧棱长都相等,底面是正方形,其主视图如图所示,该四棱锥侧面积等于( )

| A. | 20 | B. | 5$\sqrt{2}$ | C. | 4($\sqrt{5}$+1) | D. | 4$\sqrt{5}$ |
14.已知命题p:若a>b,则a2>b2;q:“x≤1”是“x2+2x-3≤0”的必要不充分条件.则下列命题是真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
4.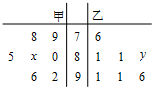 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
9.某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
哈尔滨市某月AQI指数频数分布如下表2:
(1)设x=$\frac{M}{100}$,根据表1的数据,求出y关于x的回归方程;
(参考公式:$\hat y=\hat bx+\hat a$;其中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\overline a=\overline y-\hat b\overline x$)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
| M | 900 | 700 | 300 | 100 |
| y | 0.5 | 3.5 | 6.5 | 9.5 |
| M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
(参考公式:$\hat y=\hat bx+\hat a$;其中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\overline a=\overline y-\hat b\overline x$)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
 如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.
如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.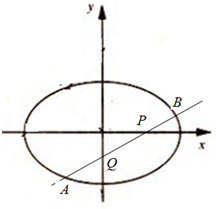 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.